j'ai besoins de votre aide.
Dans le cadre de un de mes projet, je dois trouver la solution fondamental de l'eq de la chaleur et biensur le prouver.
Pouvez-vous m'aider?
Merci
Equation de la chaleur
11 messages
- Page 1 sur 1
sur un ouvert quelconque tu peux utiliser le theoreme de hille yoshida
il doit marcher aussi sur R
sinon en effet par fourier regarde ici
il doit marcher aussi sur R
sinon en effet par fourier regarde ici
Pour respecter la charte, je ne te donne pas toute la solution, mais quelques indices en te laissant le soin de faire les calculs :
soit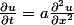
En différentiant :)
et plus généralement :
)
Pour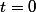 on a
on a 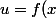) et donc
et donc_0=af"(x))
et plus généralement :
_0=a^nf^{(2n)}(x))
Si on admet que la solution est dévellopable en série de Mac Laurin, on peut l'écrire sous la forme :
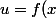+\frac{at}{1!}+...+\frac{a^nt^n}{n!}f^{(2n)}(x)+...)
Tu as aussi la solution de Poisson :
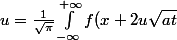e^{-u^2}du)
Tu vérifieras qu'elle satisfait à l'équation et aux conditions initiales
soit
En différentiant :
et plus généralement :
Pour
et plus généralement :
Si on admet que la solution est dévellopable en série de Mac Laurin, on peut l'écrire sous la forme :
Tu as aussi la solution de Poisson :
Tu vérifieras qu'elle satisfait à l'équation et aux conditions initiales
au fait, tout ca j'ai deja.
j'ai ma solution fondamental et je dois prouver qu'elle l'est.
Si ca te dit, regarde ce qu' j'ai http://matwww.ee.tut.fi/matematiikka_beta/wp-content/uploads/2008/05/di_alexane_verraux.pdf
page 26.
mais je n'arrive pas a prouver formellement qu'elle est bien solution
Merci
j'ai ma solution fondamental et je dois prouver qu'elle l'est.
Si ca te dit, regarde ce qu' j'ai http://matwww.ee.tut.fi/matematiikka_beta/wp-content/uploads/2008/05/di_alexane_verraux.pdf
page 26.
mais je n'arrive pas a prouver formellement qu'elle est bien solution
Merci
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 34 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
