Enveloppe convexe !
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 16 Juil 2007, 16:30
par barbu23 » 16 Juil 2007, 16:30
oui mais il faut un petit raisonnement mathématique rigoureux pour ça, c'est pas très clair !!!
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 16 Juil 2007, 16:35
par barbu23 » 16 Juil 2007, 16:35
moi, je suis pas encore tout à fait convaincu de ce raisonnement ... il faut encore le démontrer avec des expressions mathematiques...etc !!
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 16 Juil 2007, 18:23
par barbu23 » 16 Juil 2007, 18:23
J'ai enfin trouvé la solution :
L'inclusion reciproque repose sur le résultat suivant que j'ai déjà montré au début de ce topic !!
Soit

un convexe tel que :
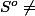
.
Si :
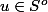
et
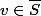
alors l'ensemble :
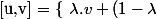. u / \lambda \in [0,1] \} $)
est contenu dans :
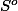
.
Revenons à l'inclusion:

:
Soit:
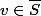
et
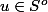
.
Alors:
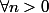
:
.v \in S^{o} $)
.
D'après le résultat du début de ce topic :
.v \in \overline{S^{o}} $)
CQFD.
-
kazeriahm
- Membre Irrationnel
- Messages: 1608
- Enregistré le: 04 Juin 2006, 09:49
-
 par kazeriahm » 16 Juil 2007, 18:41
par kazeriahm » 16 Juil 2007, 18:41
barbu23 a écrit:Si :
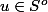
et
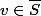
alors l'ensemble :
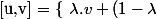. u / \lambda \in [0,1] \} $)
est contenu dans :
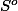
.
.
si lambda vaut 1 alors tu obtiens que v S°, ca me parait douteux
d'ailleurs c'est la solution proposée par aviateur
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 16 Juil 2007, 19:05
par aviateurpilot » 16 Juil 2007, 19:05
kazeriahm a écrit:si lambda vaut 1 alors tu obtiens que v S°, ca me parait douteux
d'ailleurs c'est la solution proposée par aviateur
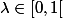
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 16 Juil 2007, 19:08
par barbu23 » 16 Juil 2007, 19:08
oui , on exclut alors :
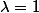
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 18 Juil 2007, 15:00
par barbu23 » 18 Juil 2007, 15:00
Bonjour:
J'aimerai que vous m'aidiez à resoudre ce petit exo ... je ne vois pas comment faire ... !!!
Soit
 $)
.
Soit
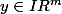
.
Soit:
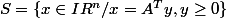
.
Montrer que :

est convexe et fermé.
merçi infiniment !!!
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 18 Juil 2007, 15:08
par barbu23 » 18 Juil 2007, 15:08
Pour

convexe, ce n'est pas dur !!
Soient :
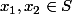
.
Soit:
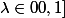
:
On a:
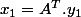
et
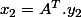
avec:
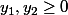
.

.x_{2} = \lambda A^{T}.y_{1} + A^{T}.(1-\lambda).y_{2} = A^{T}.(\lambda.y_{1} + (1-\lambda).y_{2}) $)
avec:
.y_{2} \geq 0 $)
.
Par conséquent :

est convexe.
Maintenant, il reste à montrer que :

fermé !
-
kazeriahm
- Membre Irrationnel
- Messages: 1608
- Enregistré le: 04 Juin 2006, 09:49
-
 par kazeriahm » 18 Juil 2007, 17:02
par kazeriahm » 18 Juil 2007, 17:02
c'est quoi A^T et y>=0 ca veut dire quoi ?
-
Alpha
- Membre Complexe
- Messages: 2176
- Enregistré le: 21 Mai 2005, 11:00
-
 par Alpha » 18 Juil 2007, 17:55
par Alpha » 18 Juil 2007, 17:55
En tout cas, n'oubliez jamais qu'il faut toujours remettre une lettre d'excuses à une enveloppe convexe.
:ptdr:
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 18 Juil 2007, 17:57
par barbu23 » 18 Juil 2007, 17:57
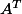
est la transposée de

.

est un vecteur de
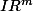
, tel que toutes ses composantes sont positives !!
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 18 Juil 2007, 19:57
par barbu23 » 18 Juil 2007, 19:57
:help: svp !!
-
kazeriahm
- Membre Irrationnel
- Messages: 1608
- Enregistré le: 04 Juin 2006, 09:49
-
 par kazeriahm » 18 Juil 2007, 21:55
par kazeriahm » 18 Juil 2007, 21:55
si tu enlèves la condition y>=0, ton ensemble est un ev de dimension finie (Im(A transposée)) donc fermé
il doit y avoir quelque chose dans ce gout la mais je vois pas (en fait je pense qu'il faut regarder ce que y>=0 entraine sur x et en déduire une propriété de l'ensemble, le voir comme l'intersection de cet ev et d'un autre ensemble fermé... peut etre que pas du tout)
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 19 Juil 2007, 21:15
par barbu23 » 19 Juil 2007, 21:15
Combien y'a-t-il de méthodes pour montrer qu'un ensemble est fermé ?!
et merçi d'avance !!
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 19 invités
