Entiers de Gauss

[j4n]

Je bloque sur pas mal de questions, je commence avec la première, si certains veulent m'aider sur la suite, ce serait avec plaisir.

On travaille donc sur les entiers de Gauss; l'ensemble Z[i] = {a+ib | a,b \in Z }

Ce que l'on sait ou avons démontré:

- Z[i] est un sous-anneau de C
- |x²| \in N
- U(Z[i]) = {+/- i ; +/- 1 } = {z \in Z[i] | |z²|=1}
- On dit que x divise y si: il existe k dans Z[i] tel que y=kx
- x est associé à y: il existe un élément de u \in U(Z[i]) tel que y=ux
- On dit que x est irréductible dans Z[i] si x n'est pas inversible et que ses seuls diviseurs sont 1,x et ses associés.


On prend maintenant un ensemble de représentants des classes d'équivalence des irréductibles de Z[i] pour la relation d'association telle que:
- tout élément de P est irréductible
- tout irréductible de Z[i] est associé à un élément de P
- les éléments de P ne sont pas associés deux à deux


Question
Montrer que: Pour tout éléments de Z[i] différents de 0, il existe 1 élément de U(Z[i]) et une famille presque nulle (\alpha p)p\in P d'entiers naturels pour lesquels

u \prod_{p \in P}^{}{p^{\alpha_{p}}}

[GaBuZoMeu]

On dit que x est irréductible dans Z[i] s'il x n'est pas inversible et que ses seuls diviseurs sont 1,x et ses associés.

Ce n'est pas tout à fait ça : parmi les diviseurs, il y a toujours aussi les éléments inversibles. La définition la plus nette est : est irréductible si n'est pas inversible et pour toute factorisation , soit soit est inversible.

Pour ta question, on peut la résoudre par récurrence sur le carré de la norme de l'élément (qui est un entier, comme tu le sais).

[j4n]

Pour ce qui concerne la phrase, j'avoue que c'est celle du sujet.

Merci pour l'indication je vais regarder cela.
PS: désolé pour les expressions, je n'avais pas vu qu'elles n'avaient pas été transformées.

[GaBuZoMeu]

Si tu veux que tes formules latex soient compilées, il est nécessaire de les placer entre balises "tex" (dans la fenêtre d'édition complète).

[j4n]

merci!

J'avoue bloquer sur la récurrence, on suppose qu'x peut être sous forme d'un produit. Mais au rang (p+1)?

[GaBuZoMeu]

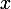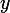Pour la récurrence : ou bien est irréductible, ou bien on peut écrire où ni ni ne sont irréductibles [c'est une erreur : je voulais en fait écrire "inversibles"]. Que peux-tu dire alors de et par rapport à ?

[j4n]

Sans mentir, je comprends pas trop la nouvelle définition que vous m'avez donné. Plus généralement j'ai beaucoup de mal avec le concept général des entiers de Gauss.

[GaBuZoMeu]

Ça va mieux une fois mon lapsus corrigé dans le message plus haut ?

[j4n]

Oui c'est pour ça que je comprenais pas. Je regarde à nouveau