quelqu'un qui peut me verifié cette demonstartion
Q : montrer que C ( ensembles des nombres complexes est un corps )
bon ce que j'ai fait
on pose pour tout 2 couples de reels (x,y) et (x',y')
(x,y)+(x'+y')=(x+x',y+y')
(x,y) x ( x',y')= (xx'-yy',x'y+xy')
on note (x,y)=x+iy et (x',y')=x'+iy'
(x+iy) x ( x'+iy') = (xx'-yy)+i(xy'+x'y)
on verifie que R² avec les lois "+" et "x" est un coprs
?????????????????
C ensm.nombres complexes est un corps
8 messages
- Page 1 sur 1
On considère un groupe G muni d'une loi de composition interne T :
G admet un élément neutre e; tout élément a de G admet un symétrique a' tel que aTa'=e élément neutre de l'ensemble E.
pour la loi +, l'élément neutre que tu as identifié bien sûr étant le coupe (0;0) le symétrique de (x;y) c'est donc (-x;-y)
G admet un élément neutre e; tout élément a de G admet un symétrique a' tel que aTa'=e élément neutre de l'ensemble E.
pour la loi +, l'élément neutre que tu as identifié bien sûr étant le coupe (0;0) le symétrique de (x;y) c'est donc (-x;-y)
stephaneenligne a écrit:On considère un groupe G muni d'une loi de composition interne T :
G admet un élément neutre e; tout élément a de G admet un symétrique a' tel que aTa'=e élément neutre de l'ensemble E.
pour la loi +, l'élément neutre que tu as identifié bien sûr étant le coupe (0;0) le symétrique de (x;y) c'est donc (-x;-y)
Oui , mais je parle de la loi " x " ( multiplication ) ...
Bonjour.
Ambiguïté de notation.
Pour quelqu'un qui connait déjà la construction de à partir de
à partir de  , il n'y a pas de risque de confusion entre le nom de la 1ère composante x et le signe de la multiplication noté encore x, mais certainement pas pour ceux qui voient la construction pour la 1ère fois , il fallait différencier les deux. De plus on a fait un abus de notation puisqu' on a noté par "+" aussi bien l'addition usuelle de
, il n'y a pas de risque de confusion entre le nom de la 1ère composante x et le signe de la multiplication noté encore x, mais certainement pas pour ceux qui voient la construction pour la 1ère fois , il fallait différencier les deux. De plus on a fait un abus de notation puisqu' on a noté par "+" aussi bien l'addition usuelle de  que l'addition dans \mathbb{R}^2
que l'addition dans \mathbb{R}^2
Ce qu'on montre effectivement c'est , muni de ces 2 lois est bien un corps.
, muni de ces 2 lois est bien un corps.
Il faut expliquer encore pourquoi on écrit et d'où provient la notation
et d'où provient la notation 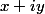
Ambiguïté de notation.
Pour quelqu'un qui connait déjà la construction de
Ce qu'on montre effectivement c'est
Il faut expliquer encore pourquoi on écrit
Bonjour.
A ce niveau, la construction de n'est pas terminée, il est prématuré de parler du nombre complexe
n'est pas terminée, il est prématuré de parler du nombre complexe  et de son conjugué
et de son conjugué 
stephaneenligne a écrit:dans un corps tout élément non nul admet un inverse, donc il faut en effet établir l'inverse de (x,y). pour tout complexe non nul 1/z=z barre / |z|²
ainsi l'inverse de (x,y) est (x/(x²+y²);-y/(x²+y²))
A ce niveau, la construction de
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 33 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
