Ensembles déduits d'autres ensembles

[laieh]

Bonjour,

Je sollicite votre aide sur un exemple de mon exercice (j'essaye de me remettre à niveau), la lecture du cours n'ayant pas suffit!

A = {(p, q)/pq −1/2q²>0}
B = {(p, q)/pq −1/3q^3>0}

On me demande de déterminer les natures suivantes :

Nature de A ∪ B :
Nature de A ∩ B :

Pouvez-vous m'aider ? Merci d'avoir lu.

[Ben314]

Erreur...

[laieh]

Effectivement, j'ai oublié des éléments importants ...

Ici, on travaille dans R ²= {(x, y)/x ∈ R, y ∈ R}

Nous devons les représenter dans R², puis les représenter dans A ∩ B et A ∪ B en indiquant leur nature particulière.

Merci de ta réponse

Edit : ou dans R²+ = {(p, q)/p ∈ R+, q ∈ R+}

[Ben314]

Si on est dans et surtout si on demande des dessins, ça me semble un peu plus pratique (*) de dire que
.
Ensuite, de tracer AnB et AuB une fois A et B tracés, ça sera complètement évident.
Concernant par exemple A, vu que pour avoir le signe d'un produit, il suffit de connaître le signe des différents facteurs, on a fortement intérêt à écrire puis à commencer par représenter les (x,y) tels que ainsi que ceux tels que pour en déduire la représentation de A.
Idem pour B.

(*) Ca ne change évidement rien au problème, mais on a plus l'habitude de visualiser avec les axes qui s'appellent "x" et "y" plutôt que "p" et "q".

[laieh]

C'est rédigé comme cela dans mon exercice ...
Vous pourriez me montrer à quoi correspond A une fois représenté ?
J'ai vraiment du mal

[Ben314]

Faire un dessin, ça me gonfle franchement (surtout vu la simplicité du bidule).
- Les points (x,y) tels que , c'est à dire c'est ceux qui sont en dessous de la droite D d'équation y=2x (y compris ceux situés sur D).
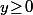
- Les points (x,y) tels que , c'est évidement ceux au dessus de l'axe des x (y compris ceux sur l'axe).
- Les points de A, c'est à dire les (x,y) tels que sont ceux ou les deux facteurs sont positifs, c'est à dire les points en dessous de D et au dessus de l'axe des x ainsi que ceux où les deux facteurs sont négatifs, c'est à dire les points au dessus de D et en dessous de l'axe des x. (les points situés sur D ou sur l'axe des x sont dans A vu que dans ce cas, le produit est nul donc est bien supérieur ou égal à 0)

=> Tu trace la droite D et l'axe des x et tu hachure les deux "régions" qui correspondent à l'ensemble A :
(en dessous de D et au dessus de l'axe des x) ainsi que (au dessus de D et en dessous de l'axe des x)

[laieh]

Je ne comprends pas comment tu passes de (x,y)/xy - 1/2y²⩾0
à x-1/2y ⩾0 et y⩾0
de même que l'aboutissement à y(x-1/2y)⩾0

[laieh]

Et aussi, en dessous de la droite D et au dessus de l'axe des x, ça ne revient pas à la même chose ?

[Ben314]

1) Le fait que xy - 1/2y² = y(x-1/2y) ça s'apelle une "factorisation" (normalement vu au collège)
2) Et le fait que pour trouver le signe d'un produit, il suffit de connaître le signe des différents facteurs, ça s’appelle "la règle des signe" (et normalement, c'est aussi vu au collège)

De plus, j'ai jamais écrit que y(x-1/2y)⩾0 c'était équivalent à (x-1/2y ⩾0 et y⩾0).
Ce que j'ai écrit, c'est que le produit (de y et de x-1/2y) est positif, si (et seulement si) les deux facteurs (y et x-1/2y) sont de même signe (règle des signes), c'est à dire tout les deux positifs OU BIEN tout les deux négatifs.

[laieh]

(p.q)/ pq

ça me bloque, ici pq = p*q ?
ou ça veut dire (p,q) diviser par pq ?
sûrement une question bête, mais dans mes énoncés tous les diviser sont écrit avec /

[jlb]

Ici, "/" signifie" tel que". Tu cherches les couples "(p;q) tels que p*q…."

[laieh]

j'ai honte lol, et pq signifie bien p*q

[jlb]

oui! oh, tu sais, il ne faut pas avoir honte de chercher à comprendre,et essaie de progresser en permanence. Bon courage.

[laieh]

Oui tqt merci ^^

Mais pourquoi doit-on hachurer aussi la zone située en dessous de l'axe des abscisses et la zone située au dessus de la droite D ? Cela revient à hachurer absolument tout?

[jlb]

Bon, je ne vais faire que reprendre ce que t'as dit Ben, si tu es d'accord, tu me réponds au fur et à mesure quand c'est bon pour toi.
Je commence: xy -1/2y² = y(x-1/2y) =>0 équivaut à (y=>0 et x-1/2y=>0) ou (y=<0 et x-1/2y=<0) ( c'est la règle des signes +*+=+ et -*-=+)

[laieh]

Oui, j'ai compris pour ça

[jlb]

Alors on continue!!! On va représenter les deux morceaux: il faut que y=>0 ET x-1/2y=>0. Tu cherches des points à ordonnées (y) positives dont les coordonnées vérifient x-1/2y=>0.

Du coup,comme les pts vérifiant x-1/2y=>0 sont d'un "côté ou de l'autre" de la droite d'équation x-1/2y=0, tu traces la droite et tu regardes le "bon" côtés de la droite.

Au final, si tu colories en rouge les points tels que y=>0 et en bleu les ponts tels que x-1/2y=>0, les points recherchés sont ceux coloriés en bleu et rouge.

[laieh]

Là je ne comprends pas, en effet les points tels que y=>0 représenteraient l'ensemble de l'axe des ordonnées ? Pourtant ils vérifient x-1/2y=> que pour un certain x chacun ?

Pour moi l'ensemble A vaudrait ça :
http://zupimages.net/viewer.php?id=18/41/lv3d.png

[jlb]

Oui, c'est ce que je t'ai décrit: en bleu sur ton dessin, tu as bien les points (x;y) qui ont une ordonnée positive ET qui sont "en dessous" de la droite x-1/2y=0, c'est à dire ceux qui vérifient aussi x-1/2y=>0. On est d'accord? Mais l'ensemble A est aussi composé des y<=0 et x-1/2y<=0. Il te reste à trouver cette autre partie.

[laieh]

Si ça doit être inférieur ou égal à 0, on trouve ça :
http://zupimages.net/viewer.php?id=18/41/wc2c.png
?