[Arithmetique] Divisibilité !

[Delroth]

Bonjour à tous,

Je suis nouveau sur ce forum et je trouve ce forum assez intéressant !

Voilà ma deuxième question qui portera sur l'arithmétique :

Soit n appartenant à N*. Montrer que le produit de n entiers naturels consécutifs est divisible par n!.

Quelqu'un saurait m'aider ? :we:

[abcd22]

Bonsoir,
Tu peux commencer par le cas où n = 2, une fois qu'on a l'idée ça se généralise facilement : pourquoi le produit k(k + 1) avec k un entier naturel est-il forcément divisible par 2 ?

[yos]

Difficile cependant d'éviter le tour de passe passe .

[Delroth]

k(k + 1) : Si k est impair, ca fait impair*pair = pair. Si k est pair, ca fait pair*impair = pair. Donc dans les deux cas divisible par 2 !

Mais en quoi ca nous aide à résoudre l'histoire ?

@yos : C'est sensé être un tour de passe ça ? :euh:

[yos]

C'est sensé être un tour de passe ça ?

de passe-passe!!
J'écris que le quotient de n entiers consécutifs par n! est un entier. Ca répond à ta question non?

[leon1789]

Il faut montrer que n! divise d(d-1)...(d-n+1)


méthode 1 :
D'un ensemble E à n éléments vers un ensemble F à d éléments, il y a d(d-1)...(d-n+1) injections. Par ailleurs, pour construire une injection f de E dans F, il suffit de choisir une partie de F à n éléments (ce sera l'image de f), puis d'associer les éléments de E à ceux de la partie choisie : disons qu'il y a X choix possibles pour l'image de f, puis n! manière d'associer les éléments de E à ceux de la partie choisie. Ainsi d(d-1)...(d-n+1) = X . n!

Remarque : .


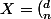méthode 2 :



ce qui invite à réaliser une récurrence (sur les deux entiers n et d)

Remarque : il s'agit du triangle de Pascal