Divergence d'une série

[log86]

Bonjour, je voudrais montrer que la série de terme général (n>=1) est divergente.
La première chose que j'ai fait c'est de regarder si elle n'était pas grossièrement divergente mais ce n'est pas le cas puisque lim (n tends vers +infini) =0
J'ai essayé d'Alembert mais je n'arrive pas à aboutir.
Pourriez vous m'aider s'il vous plait ?
Merci

[le_fabien]

Bonjour, je voudrais montrer que la série de terme général [/TEX] (n>=1) est divergente.
La première chose que j'ai fait c'est de regarder si elle n'était pas grossièrement divergente mais ce n'est pas le cas puisque lim (n tends vers +infini) =0
J'ai essayé d'Alembert mais je n'arrive pas à aboutir.
Pourriez vous m'aider s'il vous plait ?
Merci

Bonjour,
et si tu utilisais que

[leon1789]

Moi, je calculerais un équivalent du terme général en écrivant 4n+1= (4n-1) +2, etc.

[digardel]

ln(4n+1/4n-1)=ln(1+3/(4n-1))

[le_fabien]

Oui, je pense que mon idée ne va pas aboutir...
C'était une idée :blah:

[leon1789]

ln(4n+1/4n-1)=ln(1+3/(4n-1))

+2/(4n-1)

Oui, je pense que mon idée ne va pas aboutir...
C'était une idée :blah:

tu veux faire apparaitre une somme téléscopique ? c'est possible en effet.

[log86]

Bonjour à tous et merci de bien vouloir m'aider.
Je pense avoir compris la proposition de digardel mais est ce que vous pourriez me dire si ce que je dis est bon s'il vous plait; j'ai toujours du mal à expliquer avec les équivalents. Merci
J'ai =qui est équivalent à
Mais est ce que je peux dire que est équivalent à ? Pour moi oui car lim (n tend vers l'infini) *=1
or =
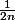
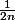
Donc est équivalent à qui est le terme général d'une série divergente. Donc notre série diverge

[leon1789]

Bonjour à tous et merci de bien vouloir m'aider.
Je pense avoir compris la proposition de digardel mais est ce que vous pourriez me dire si ce que je dis est bon s'il vous plait; (...) Donc notre série diverge

pour moi, c'est parfait !

[log86]

merci beaucoup leon1789

[charlol]

Salut , moi je pensais faire comme ça :
Je ne sais pas faire les symboles somme et produit dsl ...
;) sous entendra "somme pour k allant de 1 a n"
et ;)"produit pour k allant de 1 a n"
;)n€IN , ;)ln((4k+1)/(4k-1))=ln (;)(4k+1)/(4k-1) )
=ln ( ;)(4k+1) / ;)(4k-1) )
or ;)(4k+1)= ;)(4k-1+2)>;)(4k-1)+ 2/3 (;)(4k-1)) +2/7 (;)(4k-1)) + ... +2/4k-1 (;)(4k-1))
>;)(4k-1)[ 1+2;) (1/(4k-1))]

donc ;)(4k+1) / ;)(4k-1) > 1+2;) (1/(4k-1))
or 2;) (1/(4k-1))>;) (1/(4k))>1/4 ;) (1/(k) qui diverge(+00)
donc ;)(4k+1) / ;)(4k-1) diverge (+00)
ainsi ln ( ;)(4k+1) / ;)(4k-1) ) diverge d'ou ce qu'on voulait

Charlol

[Clembou]

Salut , moi je pensais faire comme ça :
Je ne sais pas faire les symboles somme et produit dsl ...
sous entendra "somme pour k allant de 1 a n"
et "produit pour k allant de 1 a n"
n€IN , ln((4k+1)/(4k-1))=ln (;)(4k+1)/(4k-1) )
=ln ( (4k+1) / (4k-1) )
or (4k+1)= (4k-1+2)>;)(4k-1)+ 2/3 (;)(4k-1)) +2/7 (;)(4k-1)) + ... +2/4k-1 (;)(4k-1))
>;)(4k-1)[ 1+2;) (1/(4k-1))]

donc (4k+1) / (4k-1) > 1+2;) (1/(4k-1))
or 2;) (1/(4k-1))>;) (1/(4k))>1/4 (1/(k) qui diverge(+00)
donc (4k+1) / (4k-1) diverge (+00)
ainsi ln ( (4k+1) / (4k-1) ) diverge d'ou ce qu'on voulait

Charlol

Note LaTeX : Pour des symboles produit et somme, on utilise \sum et \prod et \ln permet d'avoir un ln droit dans la formule.

Charlol, un conseil. Mets toi au LaTeX, tu verras que la présentation de ta "démonstration" sera amélioré. :++: