Dimension de intersection des Esp.affine

par **adamNIDO** » 10 Déc 2014, 17:26

Bonjour

dabord o, voit que P1 P2 P2 sont des sous espace affine de R3

do,c il suffit de verifier que P1 P2 P3 sont indepande )

soit P1=Ker f1 (d'une forme lineaire non nulle) P2=Ker f2(d'une forme lineaire non nulle) P3=Ker f3 (d'une forme lineaire non nulle) et montre que leur f lineare sont indepandante ( P1P2P3 sont indepande )
ce qui revient a discuter a b c alpha beta

sil vous plait si quelqu'un a le temps de me propose dune solution detaille car meme j'ai des indication je peux pas procede

merci pour votre aide

par **adamNIDO** » 10 Déc 2014, 20:04

Par exemple pour P1

on peut considère que

avce

on doit montrer que

est f.lineaire non nulle

si

c'est S.E.V

mais je peux pas continue j'ai besoin de quelqu'un de m'aide pour faire une redaction de solution de ce type dexercice
merci pour votre aide

par **capitaine nuggets** » 10 Déc 2014, 20:32

Salut !

adamNIDO a écrit:Bonjour

est ce que on doit montrer dabord que P1 P2 P2 sont des sous espace affine de R3 puis en fait lintersection des ces espace forme un sous espace affine et par suite on peut calculer la dimension de leur intersection

et pour faire ca P1 pour que soit un S.E.A on doit la montrer que P1=Ker (d'une forme lineaire non nulle)
de meme pour P2 P3 ce qui revient a discuter a b c alpha beta

sil vous plait si quelqu'un a le temps de me propose dune solution detaille car meme j'ai des indication je peux pas procede

merci pour votre aide

A priori, l'énoncé affirme que les plans

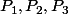
sont bien des plans affines.
Ensuite, je pense qu'on doit pouvoir raisonner sur les vecteurs normaux de ces trois plans : peut-être qu'en étudiant leur déterminant...

par **adamNIDO** » 10 Déc 2014, 21:07

capitaine nuggets a écrit:Salut !

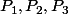
A priori, l'énoncé affirme que les plans sont bien des plans affines.
Ensuite, je pense qu'on doit pouvoir raisonner sur les vecteurs normaux de ces trois plans : peut-être qu'en étudiant leur déterminant...

Bonsoir,

le professeur de mon ami qui m'a envoyer cet exercice ma dit que leur professeur demande de montrer que

sont d'abord des sous espace affine

par **adamNIDO** » 10 Déc 2014, 21:46

capitaine nuggets a écrit:Salut !

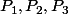
A priori, l'énoncé affirme que les plans sont bien des plans affines.
Ensuite, je pense qu'on doit pouvoir raisonner sur les vecteurs normaux de ces trois plans : peut-être qu'en étudiant leur déterminant...

oui sont des hyerplans mais on doit vérifier que leur forme linaires sont indépendante

donc on doit discuter selon a b c alpha beta theta

par **adamNIDO** » 11 Déc 2014, 21:53

Bonjour j'ai trouve la solution de ce document mais que indication pas une redaction

ils ont dit que lintersetcion cest la solution de ce system

quelqu'un pouvez vous m'explique pourquoi ca

merci d'avance

par **Ben314** » 12 Déc 2014, 08:40

Salut,
Ca veut dire quoi qu'un point (x,y,z) est dans P1 ? dans P2 ? dans P3 ?
donc...

par **adamNIDO** » 12 Déc 2014, 16:43

Ben314 a écrit:Salut,
Ca veut dire quoi qu'un point (x,y,z) est dans P1 ? dans P2 ? dans P3 ?
donc...

Bonjour Monsieur Ben

j'ai pu contacté L'enseignante auteur de l'exercice a savoir madame Marie-Claude David

Un point de coordonnées (x,y,z) appartient à l'intersection des trois plans s'il vérifie les trois équations, c'est-à-dire le système Ce système se résout facilement par la méthode de Gauss. Selon les valeurs des paramètres alpha et bêta le rang r du système est différent et la dimension de F est 3 -r. Voyez http://wims.auto.u-psud.fr/wims/wims.cgi?module=U1/algebra/docsyslin.fr

Marie-Claude DAVID
mathématiques Bât. 425
Université Paris-Sud
91405 Orsay cedex

meme moi je veux proceder par la methode de que un sous espace vectoriel peut ecrire sous forme dun Ker d''une forme lineare et de montrer que les forme llineaire sotn independante

Dimension de intersection des Esp.affine

dimension de intersection des Esp.affine

Qui est en ligne