Dimension,Bases Sujet résolu

[yagami]

bonjour,

je bloque sur cette exercice,

Soit f l'application de Rn[X] dans R[X] définie en posant pour tout P(X) ∈ Rn[X] : f((P(x))=P(X+1)+(P(X-1)-2P(X).

Déterminer le noyau et l'image de f.Calculer leur dimension respective.

Merci d'avance.

[Robot]

Qu'as-tu essayé ?

[yagami]

J'ai montrer que f est linéaire et que son image et incluse dans Rn[x], ensuite j'ai claculé pour n=3,et j'ai donné la matrice dans la base 1.X .X^2 .X^3

[Robot]

Et qu'as-tu constaté ? Quel est le noyau dans ce cas ? L'image ?

[yagami]

on a ker(f)={0,0,0} et Im(f)={0,0,0}

[Robot]

Ta réponse n'est pas sérieuse.
Quelle est la matrice de f que tu as trouvée pour le cas n=3.

[yagami]

j'ai trouvé cette matrice :

(0 0 2 0)
(0 0 0 6)
(0 0 0 0)
(0 0 0 0)

[Robot]

OK.
Alors explique-moi comment tu trouves le noyau et l'image.
PS : je vais faire mon marché. Si quelqu'un veut continuer le dialogue ...

[yagami]

ker f ={ x,y,z,t) ∈ R4 / f((x,y,z,t))={(0,0,0)}

on dit que f((x,y,z))=(0,0,0) est équivalent a l'expression ci-dessous:
0x+0y+2z+0t=0
0x+0y+0z+06=0
0x+0y+0z+0t=0
0x+0y+0z+0t=0
don ker(f)={0,0,0,0}
Im (f)=((x,y,z,t)/((x,y,z,t))=(x,y,z)∈ R3}
Im(f)= x(0,0,0,0)+y(0,0,0,0)+z(2,0,0,0)+t(0,6,0,0)
donc im(f)=z(2,0,0,0)+t(0,6,0,0)= im(f)={(2,0,0,0),(0,6,0,0)}∈R3}
donc si j'ai bien compris dim ker(f) est nulle et dim de im(f) est de 2.

[Robot]

Beaucoup de choses qui ne vont pas.
1°) Le système est extrêmement simple à résoudre, et tu te plantes complètement ! Reprends ça correctement.
2°) Tu fais une confusion complète entre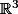 et 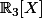qui est un espace vectoriel de base et donc de dimension 4.
3°) Ton écriture "Im (f)=((x,y,z,t)/((x,y,z,t))=(x,y,z)∈ R3}" n'a absolument aucun sens.
3°) Tu as un endomorphisme de 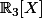, donc l'image et le noyau de sont des sous-espaces de 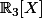. Les éléments de 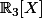sont des polynômes. donc tu dois les décrire comme ensembles de polynômes.
4°) Le théorème du rang, tu en as entendu parler ? Quelle relation donne-t-il entre la dimension de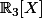 , la dimension du noyau de et la dimension de son image ?

[yagami]

oui je connais le théorème du rang dim(f)+dimker(f)=dim=dim E

ok donc l'image si j'ai bien compris c'est ker f =< 1, x >=< e0, e1 >, et Im f =< 1, x >=< e0, e1 >. f est de rang 2.

[Robot]

Eh bien, c'est le jour et la nuit. Si tu as trouvé ça tout seul, bravo.

[yagami]

merci beaucoup, je n'ai pas trouvé le réultat tout seul, mais j'ai compris coment faire.