Sujet résolu

[yagami]

bonjour,

je bloque sur un exercice,

On suppose que n est un entier non nul. Soit un échiquier ayant 2^n case par coté. On enlève une case de coin, à cet échiquier.

a) faire un dessin pour n=1.

merci d'avance

[Robot]

. C'est ça qui te bloque ?

[yagami]

je comprend pour n>=2 mais pas pour n=1

Pour moi le trimino pour n=1 a une seule case qui sert de coin, puis 2 autre.

[Robot]

Qu'est-ce que tu racontes ? Tu prends un damier de 2x2 cases et tu enlèves une case (ici toutes les cases sont des cases de coin). Il reste ...

[yagami]

ok merci , mon professeur c'est trompé ^^ sur la correction.

[Robot]

Heureusement, je connais l'énoncé : il s'agit de montrer qu'un damier de 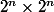cases auquel on enlève une case de coin peut être pavé par des triminos (trois cases en forme de L).
Ton professeur a peut-être commencé la récurrence à , ça marche très bien.

[yagami]

ah d'accord^^ mercie