Difféomorphisme
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
checkmaths
- Membre Relatif
- Messages: 100
- Enregistré le: 27 Mai 2017, 23:07
-
 par checkmaths » 28 Mai 2017, 16:26
par checkmaths » 28 Mai 2017, 16:26
Bonjour, je suis en train de faire un exercice tiré d'un ancien examen de Calcul Différentiel que voici :
Considérons la fonction
\longrightarrow\mathcal{M}_n(\mathbb{R}))
définie par
=A^2)
.
On sait que

est

, que
.H=HA+AH)
et que l'ensemble des points où

est étale peut s'écrire
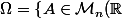\middle|\textrm{Ant}(A)=\{0\}\right\})
où
)
est l'ensemble des matrices anticommutant avec

.
Soit
)
le sous-ensemble des matrices symétriques. On pose
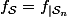
.
Rappelons à toutes fins utiles qu'une matrice symétrique  est dite : positive si
est dite : positive si 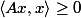 ,
, 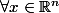 , et définie positive si
, et définie positive si 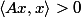 ,
, 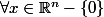 . En outre, toute matrice symétrique est diagonalisable dans une base orthonormée.
. En outre, toute matrice symétrique est diagonalisable dans une base orthonormée.1. Montrer que
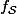
est une bijection de
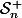
sur lui-même.
J'avoue être perdu sur ce genre de question, je ne sais jamais trop par où commencer... Pourriez-vous me donner qq pistes svp ?



Modifié en dernier par
checkmaths le 28 Mai 2017, 16:57, modifié 2 fois.

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 28 Mai 2017, 16:48
par Lostounet » 28 Mai 2017, 16:48
Bonjour,
Les matrices de Sn seraient-elles des matrices symétriques positives?
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
checkmaths
- Membre Relatif
- Messages: 100
- Enregistré le: 27 Mai 2017, 23:07
-
 par checkmaths » 28 Mai 2017, 17:12
par checkmaths » 28 Mai 2017, 17:12
Non, les matrices de

sont des matrices symétriques mais elles peuvent être positives puisque
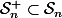
.

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 28 Mai 2017, 17:14
par Lostounet » 28 Mai 2017, 17:14
checkmaths a écrit:Non, les matrices de

sont des matrices symétriques mais elles peuvent être positives puisque
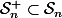
.
Ben tu viens de modifier ton message pour mettre un +

Bref, ton but est de montrer qu'à toute matrice symétrique positive S correspond une unique matrice positive M tel que M^2 = S.
Tout d'abord tu peux utiliser le fait que tout matrice symétrique est diagonalisable dans une base orthogonale (théorème spectral). Le but est de construire à S donné, un unique M. Que peux-tu dire du signe des valeurs propres de S (et de M ?)
On peut faire à part l'existence et l'unicité si tu veux.
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 28 Mai 2017, 18:10
par zygomatique » 28 Mai 2017, 18:10
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
checkmaths
- Membre Relatif
- Messages: 100
- Enregistré le: 27 Mai 2017, 23:07
-
 par checkmaths » 28 Mai 2017, 18:50
par checkmaths » 28 Mai 2017, 18:50
Parce qu'il y a une question où il faut démontrer que
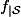
est un

-difféomorphisme de
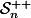
sur lui-même. Mais j'y suis pas encore...

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 28 Mai 2017, 19:42
par zygomatique » 28 Mai 2017, 19:42
et alors ? c'est le même sujet ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
checkmaths
- Membre Relatif
- Messages: 100
- Enregistré le: 27 Mai 2017, 23:07
-
 par checkmaths » 28 Mai 2017, 19:48
par checkmaths » 28 Mai 2017, 19:48
Si j'avais mis comme sujet "Difféomorphisme et applications étales", j'aurais tout mis ensemble. Mais, comme on peut pas modifier le titre du sujet... Du coup, j'ai coupé en deux pour que tout le monde y voit clair.

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 28 Mai 2017, 20:00
par Lostounet » 28 Mai 2017, 20:00
zygomatique a écrit:et alors ? c'est le même sujet ...
et si tu laissais la modération...aux modérateurs? :p
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
checkmaths
- Membre Relatif
- Messages: 100
- Enregistré le: 27 Mai 2017, 23:07
-
 par checkmaths » 28 Mai 2017, 21:08
par checkmaths » 28 Mai 2017, 21:08
En gros, pour cette q° voilà comment je procèderais :
On a :
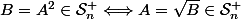
. Donc
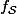
est une bijection de
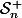
sur lui-même.
2. Montrer que
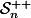
est un ouvert de

.
Les applications
)
sont continues sur

. Ainsi,
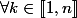
,
)
est un ouvert de

, et
})
est un ouvert de

comme une intersection finie d'ouverts.
Donc, ça c'est ok, mais c'était chaud et pas sûr que j'aurais trouvé ça en exam

3. Montrer que
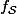
est un

-difféomorphisme de
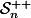
sur lui-même.
Modifié en dernier par
checkmaths le 28 Mai 2017, 21:33, modifié 1 fois.

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 28 Mai 2017, 21:14
par Lostounet » 28 Mai 2017, 21:14
checkmaths a écrit:En gros, pour cette q° voilà comment je procèderais :
On a :
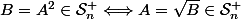
. Donc
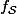
est une bijection de
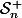
sur lui-même.
C'est quoi cette racine carrée... sur une matrice ?!
Et c'est vraiment trop rapide comme démarche... Tel quel c'est limite faux sans justification supplémentaire.
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
checkmaths
- Membre Relatif
- Messages: 100
- Enregistré le: 27 Mai 2017, 23:07
-
 par checkmaths » 28 Mai 2017, 21:35
par checkmaths » 28 Mai 2017, 21:35
La racine carrée d'une matrice symétrique positive existe et elle est aussi symétrique positive. Donc, cette notation de racine carrée existe bien, non ?

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 28 Mai 2017, 21:41
par Lostounet » 28 Mai 2017, 21:41
checkmaths a écrit:La racine carrée d'une matrice symétrique positive existe et elle est aussi symétrique positive. Donc, cette notation de racine carrée existe bien, non ?
Tu ne l'as pas démontré...
Si je te donne maintenant une matrice symétrique positive, tu peux me donner une /sa racine carrée? Et si oui... comment tu sais si elle est unique? (parler de "la" racine carrée, ça veut dire que c'est unique)
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
checkmaths
- Membre Relatif
- Messages: 100
- Enregistré le: 27 Mai 2017, 23:07
-
 par checkmaths » 28 Mai 2017, 21:47
par checkmaths » 28 Mai 2017, 21:47

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 28 Mai 2017, 21:50
par Lostounet » 28 Mai 2017, 21:50
Euh... Tu n'as-tu pas remarqué que pour le prouver, le pauvre monsieur a mis une page entière ?
On voit bien que c'est pas quelque chose de super évident. Et si c'est un examen.. tu ne peux pas écrire "racine de B" sans expliquer ce que c'est... Il parle de plus de "matrices codiagonalisables"...
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
checkmaths
- Membre Relatif
- Messages: 100
- Enregistré le: 27 Mai 2017, 23:07
-
 par checkmaths » 28 Mai 2017, 21:55
par checkmaths » 28 Mai 2017, 21:55
Ok donc, après avoir démontré que cette racine existe, on peut faire ce que j'ai fait du coup


-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 28 Mai 2017, 22:03
par Lostounet » 28 Mai 2017, 22:03
checkmaths a écrit:Ok donc, après avoir démontré que cette racine existe, on peut faire ce que j'ai fait du coup

Pas vraiment non. Il faut montrer que cette racine existe
et qu'elle est unique (et c'est plus dur !) avant de pouvoir même utiliser la notation "racine" pour une matrice symétrique positive.
Et tu vois bien que c'est pas si évident que ça, je me trompe? Si je te donne une matrice (qui remplit les hypothèses), comment tu fais pour trouver une de ses racines carrées (cela montrerait l'existence).
Si tu supposes le résultat connu (par exemple si c'est du cours), tu devrais nous le dire. Mais cela n'enlève rien au fait que c'est pas évident (et qu'on va surement pas écrire racine d'une matrice pour camoufler la difficulté de la démo).
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
checkmaths
- Membre Relatif
- Messages: 100
- Enregistré le: 27 Mai 2017, 23:07
-
 par checkmaths » 28 Mai 2017, 23:57
par checkmaths » 28 Mai 2017, 23:57
Pour la 3.,
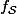
est

comme

est

,
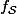
est injective, mais je n'arrive à montrer que
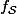
est étale sur
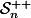
. Pourriez-vous m'aider svp ? Y'aurait-il une autre méthode ?





-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 29 Mai 2017, 12:33
par zygomatique » 29 Mai 2017, 12:33
Lostounet a écrit: zygomatique a écrit:et alors ? c'est le même sujet ...
et si tu laissais la modération...aux modérateurs? :p
il n'est pas question de modération mais de bon sens : quand un prochain étudiant fera se sujet et cherchera un fil en parlant pour de l'aide il semble évident qu'avoir un seul fil qui regroupe l'ensemble des idées et de l'aide apportée est plus pertinente ...
... sans parler du point de vu écologique et consommation d'énergie ...

Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 21 invités






sont des matrices symétriques mais elles peuvent être positives puisque
.

. Donc
est une bijection de
sur lui-même.




