Eq. Diff premier ordre
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
MacErmite
- Membre Relatif
- Messages: 408
- Enregistré le: 12 Mai 2006, 12:00
-
 par MacErmite » 05 Mar 2010, 17:43
par MacErmite » 05 Mar 2010, 17:43
Bonjour,
Je cherche à résoudre cette eq. diff :

Mais je bloque rapidement pour la résoudre.
Voilà ce que j'ai fait :

,
=Arctan(x)+c)
,
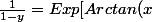]K)
,
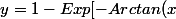].K)
Apparement ce n'est pas le bon résultat et je ne comprends pas ou est l'erreur,
pouvez-vous m'aider ?
Merci
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 05 Mar 2010, 17:47
par Nightmare » 05 Mar 2010, 17:47
Salut !
Je trouve plutôt

!
-
MacErmite
- Membre Relatif
- Messages: 408
- Enregistré le: 12 Mai 2006, 12:00
-
 par MacErmite » 05 Mar 2010, 18:08
par MacErmite » 05 Mar 2010, 18:08
En effet après correction j'obtiens
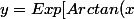].K+1)
Merci
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 05 Mar 2010, 18:10
par Nightmare » 05 Mar 2010, 18:10
Plusieurs choses dérangent dans ta solution, par exemple, elle ne donne pas la fonction y=1 qui pourtant est solution.
L'emploie du log nécessite d'avoir montré au préalable que y-1 est bien strictement positif.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 05 Mar 2010, 18:20
par Ben314 » 05 Mar 2010, 18:20
Salut, tous (encore moi !!!)
De mémoire, lorsque l'on fait se genre de calculs, on utilise trés souvent le fait que, si une fonction u ne s'annule pas sur un certain intervalle, la primitive de u'/u est ln(|u|) ce qui permet de traiter d'un seul coup les deux cas u>0 et u<0.
Bien sûr, un peu plus loin dans les calculs, on se retrouve avec du |u|=..., mais comme u est supposé dérivable donc continue, et quelle est aussi supposée ne pas s'annuler...
Conclusion, modulo de rajouter une valeur absolue dans le log (et de considérer un intervalle sur lequel y ne prend pas la valeur 1), je pense que la méthode proposée par MacErmite est suffisante.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 05 Mar 2010, 18:27
par Ben314 » 05 Mar 2010, 18:27
Je recopie les calculs de MacErmite pour donner ce qui me semble la "bonne" façon de rédiger (à débatre...)
En se placant sur un intervalle I sur lequel y ne prend pas la valeur 1, on a :

,
=Arctan(x)+c)
,
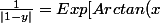+c] = Exp(c)Exp[Arctan(x)] = K.Exp[Arctan(x)])
, avec
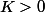
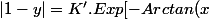])
avec

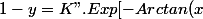])
avec

car 1-y ne change pas de signe sur I
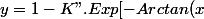])
avec

En fait, on constate que, si K"=0, cela fournit aussi une solution de l'équation (mais qui vaut 1 sur tout intervalle !)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 51 invités