Développement limités, équivalent et limite [RESOLU]

[Harmonie]

Bonjour !

J'ai une petite incompréhension sur les DL.
Lorsqu'on calcule un développement à l'ordre 2 par exemple, on obtient avec le premier terme (partie principale ) l'équivalent de la fonction. Cette équivalent correspond aussi à sa limite en 0 non ?
Mais quand ce matin j'ai demandé à mon prof si partie principale, équivalent et limite étaient la même chose il m'as dit non.. Du coup il y'a un non sens pour moi, quelqu'un pourrait m'expliquer ?

Merci :)

[BiancoAngelo]

Bonjour !

J'ai une petite incompréhension sur les DL.
Lorsqu'on calcule un développement à l'ordre 2 par exemple, on obtient avec le premier terme (partie principale ) l'équivalent de la fonction. Cette équivalent correspond aussi à sa limite en 0 non ?
Mais quand ce matin j'ai demandé à mon prof si partie principale, équivalent et limite étaient la même chose il m'as dit non.. Du coup il y'a un non sens pour moi, quelqu'un pourrait m'expliquer ?

Merci

Bonjour, d'abord, tu dois parler de DL en un point...

Donc si tu fais un DL en x=1, logique que ça ne corresponde pas à la limite en 0...
Est-ce que tu parles donc d'un DL en 0 ?

Après, ce n'est pas la même chose dans un sens d'objet je pense.
La limite ne peut pas être l'équivalent de la fonction.

Exemple, si f tend vers l'infini en 0, on ne dit pas f équivalente à . On pourrait par exemple dire que f ~ 1/x si c'est le cas.

Dans ce cas précis, ce n'est pas un DL, vu qu'un DL à un ordre n doit être un polynôme... :happy2:

Il ne faut pas confondre avec un développement asymptotique

En espérant que ça t'aide.

[Harmonie]

Coucou ! Merci de ta réponse, effectivement je parle d'un DLn(0), je n'ai pas précisé pardon.

Et oui un DLn(x) est forcement un polynôme mais par exemple pour e^x
On a DL2(0) e^x= 1 + x + (x^2)/2!
On a aussi lim e^x=1 quand x tend vers 0, et e^x est équivalent a 1 en 0 (si je ne m'abuse).
Si on prend DL2(0) cos(x) = 1 - (x^2)/2! + (x^4)/4!
En x=0, lim cos(x)=1 et on a cos(x)~1 en 0

Mais ce que je dois comprendre c'est que ça ne fonctionne pas tout le temps c'est ça ? Donc si on me demande de calculer la limite d'un fonction donnée en un point x je dois ôter de mon esprit l'idée de faire un DL ? J'avais cru comprendre qu'utiliser les DL permettait de lever d'éventuelle indeterminations pour calculer la limite.
Dans ton exemple tu parle d'une fonction qui tend vers l'infini, mais a ce moment la on n'utilise un développement assymptotique non ? (que je n'ai pas bien compris d'ailleurs) ah justement tu en as parlé a la fin de ton post je n'avais pas vu :0

[BiancoAngelo]

Coucou ! Merci de ta réponse, effectivement je parle d'un DLn(0), je n'ai pas précisé pardon.

Et oui un DLn(x) est forcement un polynôme mais par exemple pour e^x
On a DL2(0) e^x= 1 + x + (x^2)/2!
On a aussi lim e^x=1 quand x tend vers 0, et e^x est équivalent a 1 en 0 (si je ne m'abuse).
Si on prend DL2(0) cos(x) = 1 - (x^2)/2! + (x^4)/4!
En x=0, lim cos(x)=1 et on a cos(x)~1 en 0

Mais ce que je dois comprendre c'est que ça ne fonctionne pas tout le temps c'est ça ? Donc si on me demande de calculer la limite d'un fonction donnée en un point x je dois ôter de mon esprit l'idée de faire un DL ? J'avais cru comprendre qu'utiliser les DL permettait de lever d'éventuelle indeterminations pour calculer la limite.
Dans ton exemple tu parle d'une fonction qui tend vers l'infini, mais a ce moment la on n'utilise un développement assymptotique non ? (que je n'ai pas bien compris d'ailleurs) ah justement tu en as parlé a la fin de ton post je n'avais pas vu :0

En effet, pour lever les indéterminations ou même pour trouver une limite rapidement, le DL c'est top !

Admettons qu'on prenne la fonction et qu'on veuille l'étudier en 0.

On peut faire un DL de chaque fonction de la fraction.

On a d'ailleurs cos(x) ~ 1 et sin(x) ~ x.

On a alors f(x) ~ 1/x qui n'est pas un DL...

Donc on peut le faire, c'est juste que le résultat n'est pas un DL...

On trouve bien alors que la limite est infinie en 0...

[Harmonie]

D'aaaaacord ! Et du coup pour l'exemple de cotan, vu qu'on etudie au final la limite en 0 de l'équivalent ca veut dire qu'on fait un développement asymptotique ?

Si j'ai compris

Un dl en un point fini nous donne avec le 1er terme la limite de la fonction dont on a fait le dl
L'étude de l'équivalent d'une fonction rationnelle nous donne sa limite

C'est ça ou je n'y suis pas du tout ?

[BiancoAngelo]

D'aaaaacord ! Et du coup pour l'exemple de cotan, vu qu'on etudie au final la limite en 0 de l'équivalent ca veut dire qu'on fait un développement asymptotique ?

Si j'ai compris

Un dl en un point fini nous donne avec le 1er terme la limite de la fonction dont on a fait le dl
L'étude de l'équivalent d'une fonction rationnelle nous donne sa limite

C'est ça ou je n'y suis pas du tout ?

Oui c'est ça.
En fait, le seul souci dans tout ça, c'est que les fonctions n'admettent pas systématiquement un DL.
Avec le développement de Taylor, on a l'impression que tout va toujours très bien.

Mais par exemple, avec les fonctions qu'on développe en série entière avec celui-ci, on tombe des fois sur des trucs "fous" : tous les coefficients valent 0 et pourtant la fonction n'est pas nulle (c'est une fonction exponentielle particulière...). Référence : fonctions analytiques.

Tout ça pour dire que ces développements marchent bien, mais qu'il faut faire attention aux sens qu'ils ont...

On peut utiliser aussi les DL ailleurs que dans les fractions rationnelles...
Faut toujours vérifier la compatibilité avec les opérations utilisés !

De la même façon qu'on peut trouver le DL à l'ordre qu'on veut de cos(sin(x)) par exemple...

[Harmonie]

Ok super tout est clair maintenant à ce propos, merci ! Bonne jourée :)

[zygomatique]

salut

il me semble que la question que tu devrais te poser est ::

qu'est-ce qu'un développement limité ?

[Harmonie]

Bonjour !
Si j'ai compris, un développement limité est un outil mathématique, permettant de faire une bonne approche d'une fonction donnée en un point défini, il s'exprime sous la forme de somme de polynômes et on l'obtient à partir de la formule de Taylor ou alors avec des formules usuelles apprises par coeur pour exp, ln(1+x), cos/ch/sin/sh, (1+x)^(a)..

Mais enfait, ce qu'il faut je revoie et que j'applique c'est le développement asymptotique avec la formule de stirling : (n! ~ R(2*pi*n)e..(non je ne la connais pas) on ne l'as jamais utilisée, du coup je ne sais pas trop à quoi ça sert.

[zygomatique]

ça reste très imprécis ...

un développement limité est une écriture ...

c'est l'écriture (sous réserve d'existence) d'une fonction f sous la forme d'une somme d'un polynome de degré n et d'un reste qu'on écrit généralement

et il existe différentes formules de ce reste ....

dans un développement asymptotique on remplace simplement les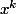 par leurs inverses ....

[Harmonie]

Effectivement, j'ai oublié le reste, mais on l'écrit toujours de la même façon, enfin on peut l'écrire comme vous l'avez écrit ou sous forme d'intégrale ou comme le produit x^n*e(x) si on effectue le développement en 0. Mais c'est pareil non ? Enfin jusqu'à présent on ne nous a pas demandé d'effectué d'opérations sur le reste du coup la notation que vous avez donné est celle que j'utilise toujours, à tord ?