Bonjour à tous,
je sèche à la dernière question d'un exercice sur les polynômes.
En voici l'énoncé :
On pose B=(X-1)^2.
1.
Effectuer la division euclidienne par B des polynômes suivants :
a) A2= 2X^3 - 3X^2 +1
b) A3 = 3X^4 - 4X^3 +1.
2. On pose An= aX^(n+1) + bX^n +1
a. Déterminer en fonction de n les réels a et b pour que B divise A.
b) Avec les valeurs de a et b trouvées ci-dessus, déterminer le polynôme quotient dans la division de An par B.
J'a trouvé et vérifié pour la 1 :
a) A2 = B(2X+1)
b) A3 = B(3X^2 + 2X +1)
et pour la 2. a) :
a= n
b= -(n+1)
Le problème c'est que je n'arrive pas à trouver mon hypothèse de récurrence pour la b)
Quand je regarde les résultats du quotient pour 1.a) et 1.b) je vois bien qu'il y a un lien entre les deux quotient, puisqu'on y a ajouté nX^n-1, mais je n'arrive pas à aller plus loin... Avez-vous des conseils à me donner?
Merci !
Léo
Déterminer un polynôme quotient
6 messages
- Page 1 sur 1
Salut,
Le (petit) soucis, c'est que l'énoncé n'est pas clair concerant la forme sous laquelle il veut qu'on donnd le quotient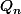 .
.
En fait, la forme la plus simple (si on doit dériver ou intégrer ou...), c'est évidement d'écrireX^n+1}{(X-1)^2}) mais ça rend la question trés con...
mais ça rend la question trés con...
Donc on va partir sur ce que tu semble vouloir obtenir, c'est à dire une formule de réccurence concernant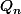 (on pourait aussi écrire
(on pourait aussi écrire 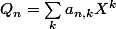 et chercher à calculer les
et chercher à calculer les 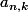 ...)
...)
Perso, j'écrirais que :
X^{n+1}-\ \ \ \ \ \ \ \ nX^n=X(X-1)^2Q_{n-1}-X)
X^n=(X-1)^2Q_n-1)
(qui proviennent de^2Q_{n-1}=XA_{n-1}) et de
et de ^2Q_n=A_n) )
)
Tu "résoud" ton système de 2 équations à 2 inconnues en regardant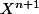 et
et 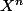 comme des inconnues que tu exprime en fonction de
comme des inconnues que tu exprime en fonction de 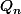 et
et 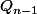 puis tu écrit que
puis tu écrit que 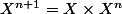 pour en déduire une formule liant
pour en déduire une formule liant 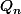 et
et 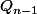 .
.
Une fois la formule finale obtenue, tu devrait sans doute constater qu'il y avait plus simple (et plus astucieux...)
Le (petit) soucis, c'est que l'énoncé n'est pas clair concerant la forme sous laquelle il veut qu'on donnd le quotient
En fait, la forme la plus simple (si on doit dériver ou intégrer ou...), c'est évidement d'écrire
Donc on va partir sur ce que tu semble vouloir obtenir, c'est à dire une formule de réccurence concernant
Perso, j'écrirais que :
(qui proviennent de
Tu "résoud" ton système de 2 équations à 2 inconnues en regardant
Une fois la formule finale obtenue, tu devrait sans doute constater qu'il y avait plus simple (et plus astucieux...)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
sticksman2 a écrit:D'accord, merci à vous deux, j'ai trouvé la solution grâce à vous !
Ben314: Je n'ai malheureusement pas trouvé une manière plus simple de trouver l' HR ( sans compter celle de Chan, que je ne vois pas comment simplifier plus !)
La méthode que je proposait fonctionne, mais ça donne une formule de récurrence entre
Vu la tête effective des Qn (donnée par chan79 dans sa première ligne et qui se conjecture façilement en calculant les 3 ou 4 premières valeurs de Qn), la formule que j'obtient n'est pas des plus pertinentes (c'est le moins qu'on puisse dire...)
Aprés, pour montrer que Qn est effectivement égal au truc en question, il y a des tas de solutions (la plus simple étant sans doute la réccurence)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 12 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
