Détermination du volume central d'un tore croisé
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
new-physician
- Membre Naturel
- Messages: 38
- Enregistré le: 17 Jan 2010, 20:42
-
 par new-physician » 27 Avr 2013, 14:28
par new-physician » 27 Avr 2013, 14:28
Bonjour,
J'ai une petite question existentielle sur un calcul de volume.
Pour former un tore on fait tourner un disque de rayon r autour d'un axe.
Le centre du disque est éloigné de l'axe de la distance R.
Dans le cas où r > R, le disque coupe l'axe et par rotation on obtient un tore un peu particulier qui est un
tore croisé.

Je cherche d'une façon ou d'une autre, pour une simulation en physique, à déterminer le volume de l'intersection (en forme de lentille) au sein du tore.
Je pensais à exprimer la courbe en coordonnées polaires et faire une intégration, ou bien d'abord calculer l'aire et l'intégrer sur 2pi.. mais je ne sais pas comment m'y prendre.
Auriez vous une idée?
En vous remerciant bien. :marteau:

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 27 Avr 2013, 15:52
par chan79 » 27 Avr 2013, 15:52
new-physician a écrit:Bonjour,
J'ai une petite question existentielle sur un calcul de volume.
Pour former un tore on fait tourner un disque de rayon r autour d'un axe.
Le centre du disque est éloigné de l'axe de la distance R.
Dans le cas où r > R, le disque coupe l'axe et par rotation on obtient un tore un peu particulier qui est un
tore croisé.

Je cherche d'une façon ou d'une autre, pour une simulation en physique, à déterminer le volume de l'intersection (en forme de lentille) au sein du tore.
Je pensais à exprimer la courbe en coordonnées polaires et faire une intégration, ou bien d'abord calculer l'aire et l'intégrer sur 2pi.. mais je ne sais pas comment m'y prendre.
Auriez vous une idée?
En vous remerciant bien. :marteau:
Salut
Essaie avec le théorème de Guldin.
J'arrive à:
volume=
-3Rr\theta))
avec

-
hammana
- Membre Relatif
- Messages: 477
- Enregistré le: 24 Avr 2012, 20:26
-
 par hammana » 27 Avr 2013, 17:54
par hammana » 27 Avr 2013, 17:54
chan79 a écrit:Salut
Essaie avec le théorème de Guldin. Ca peut se faire.
Le volume intérieur a la forme d'une perle et non d'une lentille. S'il s'agit d'une lentille optique, il faut chercher l'intersection de 2 sphères. Confirmes-tu qu'il s'agit bien d'une perle?
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 27 Avr 2013, 18:00
par Kikoo <3 Bieber » 27 Avr 2013, 18:00
hammana a écrit:Le volume intérieur a la forme d'une perle et non d'une lentille. S'il s'agit d'une lentille optique, il faut chercher l'intersection de 2 sphères. Confirmes-tu qu'il s'agit bien d'une perle?
Une perle ? Je voyais ça comme une sorte de noyau de pèche ^^ Mais on peut voir ça comme on veut, tant que cela reste un volume de révolution, non ?
Et le théorème de Guldin est alors applicable.
-
adrien69
- Membre Irrationnel
- Messages: 1899
- Enregistré le: 20 Déc 2012, 12:14
-
 par adrien69 » 27 Avr 2013, 19:21
par adrien69 » 27 Avr 2013, 19:21
Est-ce que tu as besoin d'une démonstration ? Parce que j'ai un truc qui me permet de paramétriser ta surface en polaire, mais pour la preuve...

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 27 Avr 2013, 20:05
par chan79 » 27 Avr 2013, 20:05
On peut aussi le faire par intégration.
Il faut sommer les volumes des cylindres de rayon MN et de hauteur dh quand h varie de 0 à

et multiplier par 2 ensuite.
On a

et

volume =
^2\,dh)

Sinon, je viens de voir que Serge Mehl a mis sur son site une formule pour le centre de gravité d'un segment circulaire. Ca évite trop de calculs si on le fait par Guldin :zen:

-
hammana
- Membre Relatif
- Messages: 477
- Enregistré le: 24 Avr 2012, 20:26
-
 par hammana » 28 Avr 2013, 17:38
par hammana » 28 Avr 2013, 17:38
chan79 a écrit:On peut aussi le faire par intégration.
Il faut sommer les volumes des cylindres de rayon MN et de hauteur dh quand h varie de 0 à

et multiplier par 2 ensuite.
On a

et

volume =
^2\,dh)

Sinon, je viens de voir que Serge Mehl a mis sur son site une formule pour le centre de gravité d'un segment circulaire. Ca évite trop de calculs si on le fait par Guldin :zen:

Bonsoir!
Le théorème de Guldin est intéressant quand quelqu'un (p.e. S. Mehl) a calculé pour nous la position du centre de gravité. S'il faut le faire soi-même il est plus facile de s'en passer. Dans le cas présent j'appelle u l'angle KOA et x l'angle KOM (je me réfère à la figure de Chan), V le volume, je prend le rayon pour unité, Je trouve facilement:
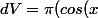-cos(u))^2cos(x)dx)
Il est possible de calculer la primitive. La seule difficulté est de calculer la primitive de cos(x)^3. (Si on est paresseux comme moi, on peut s'aider de Wolfram).
Je trouve pour le volume
/4+sin(3u)/12-ucos(u))
En calculant cette valeur pour u variant de 0 à pi/2 je trouve bien qu'elle augmente de façon monotone de 0 jusqy'à 4pi/3 (volume de la sphère de rayon 1)
Il faudrait quand même confirmer ce résultat

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 28 Avr 2013, 18:12
par chan79 » 28 Avr 2013, 18:12
Salut
On peut se passer de la formule de S. Mehl. C'est d'ailleurs ce que j'avais fait au début. Le centre de gravité G du secteur angulaire est le barycentre du centre de gravité G1 du triangle ABC et du centre de gravité G2 du segment circulaire, affectés de leurs aires. On arrive ainsi à calculer OG2.


-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 28 Avr 2013, 18:31
par chan79 » 28 Avr 2013, 18:31
hammana a écrit:Je trouve pour le volume
/4+sin(3u)/12-ucos(u))
Il faudrait quand même confirmer ce résultat
c'est bon; en tous cas, ça donne le même résultat que la formule que j'ai mise plus haut :zen:
Si on exprime le résultat en fonction de r et R, l'expression se complique.
-
new-physician
- Membre Naturel
- Messages: 38
- Enregistré le: 17 Jan 2010, 20:42
-
 par new-physician » 28 Avr 2013, 21:08
par new-physician » 28 Avr 2013, 21:08
chan79 a écrit:On peut aussi le faire par intégration.
Il faut sommer les volumes des cylindres de rayon MN et de hauteur dh quand h varie de 0 à

et multiplier par 2 ensuite.
On a

et

volume =
^2\,dh)
D'abord, merci à tous pour votre temps et votre aide grandiose.
Etant donné que je ne sais pas exploiter le théorème, je préfèrerais utiliser la méthode géométrique qui me parait plus accessible.
Mon seul problème est, qu'à cause de la racine, je n'arrive pas totalement à résoudre l'intégrale. Il me reste à intégrer une racine de (1- (h/r)^2).
J'ai cherché dans les formes d'intégrales connues, mais je n'ai pas trouvé de solution simple à cette intégrale.
Comment la résoudre?


-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 29 Avr 2013, 07:15
par chan79 » 29 Avr 2013, 07:15
bonjour
Poser x=h/r
puis
Pour intégrer

poser x= sin t
Si tu tiens à exprimer le volume en fonction de r et R, tu dois arriver au résultat ci-dessous, mais en faisant intervenir des angles comme cela a été fait précédemment, l'expression obtenue est plus simple.
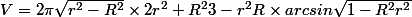)
-
new-physician
- Membre Naturel
- Messages: 38
- Enregistré le: 17 Jan 2010, 20:42
-
 par new-physician » 29 Avr 2013, 09:38
par new-physician » 29 Avr 2013, 09:38
chan79 a écrit:bonjour
Poser x=h/r
puis
Pour intégrer

poser x= sin t
Merci beaucoup...
J'ai cependant un nouveau problème lorsqu'il s'agit de determiner les nouvelles bornes d'integration lors du changement de variable x = sin t.
Si x = 0, t peut valoir 0, ou tout multiple de pi par un entier relatif...donc quelle borne inférieure choisir ?
Et la borne superieure, selon mes calculs, serait arc sin ( racine (r^2-R^2) / r ) ?
:hein:

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 29 Avr 2013, 10:22
par chan79 » 29 Avr 2013, 10:22
new-physician a écrit:Merci beaucoup...
J'ai cependant un nouveau problème lorsqu'il s'agit de determiner les nouvelles bornes d'integration lors du changement de variable x = sin t.
Si x = 0, t peut valoir 0, ou tout multiple de pi par un entier relatif...donc quelle borne inférieure choisir ?
Et la borne superieure, selon mes calculs, serait arc sin ( racine (r^2-R^2) / r ) ?
:hein:
c'est ça, j'ai fait varier t de 0 à
)
-
new-physician
- Membre Naturel
- Messages: 38
- Enregistré le: 17 Jan 2010, 20:42
-
 par new-physician » 29 Avr 2013, 10:40
par new-physician » 29 Avr 2013, 10:40
chan79 a écrit:c'est ça, j'ai fait varier t de 0 à
)
Mais la racine ne porte que sur le numérateur, non ? Moi je ne peux pas simplifier en 1-...
Cela dit, à part ca, je ne comprend pas géométriquement comment on peut simplifier le calcul de volume de la perle à un calcul de volume de cylindre fois deux. Je patauge..


-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 29 Avr 2013, 13:37
par chan79 » 29 Avr 2013, 13:37
new-physician a écrit:Mais la racine ne porte que sur le numérateur, non ? Moi je ne peux pas simplifier en 1-...
Cela dit, à part ca, je ne comprend pas géométriquement comment on peut simplifier le calcul de volume de la perle à un calcul de volume de cylindre fois deux. Je patauge..

Je te mettrai des détails dans la soirée
-
new-physician
- Membre Naturel
- Messages: 38
- Enregistré le: 17 Jan 2010, 20:42
-
 par new-physician » 29 Avr 2013, 14:35
par new-physician » 29 Avr 2013, 14:35
chan79 a écrit:Je te mettrai des détails dans la soirée
Merci. En fait nous sommes deux à avoir regardé l'intégration et on ne comprend pas le premier changement de variable non plus en x = h/r sachant que devant la racine il y a encore un r qui reste, donc on ne s'en sort jamais... :marteau:
Ca serait super si vous pouviez detailler, je ne m'en sors plus!
:doh:

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 29 Avr 2013, 17:58
par chan79 » 29 Avr 2013, 17:58
new-physician a écrit:Merci. En fait nous sommes deux à avoir regardé l'intégration et on ne comprend pas le premier changement de variable non plus en x = h/r sachant que devant la racine il y a encore un r qui reste, donc on ne s'en sort jamais... :marteau:
Ca serait super si vous pouviez detailler, je ne m'en sors plus!
:doh:

r et R sont constants
le rayon des cylindres est

(voir plus haut)
Comme

, on a bien:
volume =
^2\,dh)
le 2 vient du fait qu'on fait la somme des volumes des cylindres de hauteur dh dessinés ci-dessus et qu'il y a aussi les symétriques en dessous que je n'ai pas dessinés.
On développe le carré, ce qui revient à faire plusieurs calculs d'intégrales.
Dis moi où ça bloque par la suite.
-
new-physician
- Membre Naturel
- Messages: 38
- Enregistré le: 17 Jan 2010, 20:42
-
 par new-physician » 29 Avr 2013, 21:13
par new-physician » 29 Avr 2013, 21:13
chan79 a écrit:Dis moi où ça bloque par la suite.
Merci beaucoup. Le dessin est super! :lol3:
Mais en fait mon souci principal est autre. En effet j'ai développé le carré dans l'intégrale et faisant comme ça il y a une partie simple à intégrer qui s'additionne à une intégrale plus complexe avec la racine.
Maintenant je bloque au niveau du changement de variable x = h /r sous la racine. En effet devant la racine j'arrive à ce qu'il me reste un r^2, donc je devrais aussi le modifier selon le changement de variable...mais si je fais ça je tourne en rond. :marteau:

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 29 Avr 2013, 21:44
par chan79 » 29 Avr 2013, 21:44
new-physician a écrit:Merci beaucoup. Le dessin est super! :lol3:
Mais en fait mon souci principal est autre. En effet j'ai développé le carré dans l'intégrale et faisant comme ça il y a une partie simple à intégrer qui s'additionne à une intégrale plus complexe avec la racine.
Maintenant je bloque au niveau du changement de variable x = h /r sous la racine. En effet devant la racine j'arrive à ce qu'il me reste un r^2, donc je devrais aussi le modifier selon le changement de variable...mais si je fais ça je tourne en rond. :marteau:
Je complète demain :lol3:
-
new-physician
- Membre Naturel
- Messages: 38
- Enregistré le: 17 Jan 2010, 20:42
-
 par new-physician » 29 Avr 2013, 21:55
par new-physician » 29 Avr 2013, 21:55
chan79 a écrit:Je complète demain :lol3:
Merci, j'attends tout ça avec grande impatience, je me demande vraiment comment résoudre cette intégrale

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 46 invités





