Dérivée de e cos wt + r
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
onizuka1990
- Messages: 4
- Enregistré le: 15 Jan 2013, 09:52
-
 par onizuka1990 » 15 Jan 2013, 10:06
par onizuka1990 » 15 Jan 2013, 10:06
Bonjour,
J'ai un peu de mal à calculer la dérivée de
 = e cos (wt) + r)
, ça fait longtemps que j'ai pas abordé les dérivées.
Je me rapelle que
' = -u' sin u)
donc logiquement
)' = -w sin (wt))
Quelqu'un pourrait m'expliquer la résolution complète de cette dérivée svp ?
Au final je trouve
=-ewsin(wt))
mais je doute.
PS : Je dois aussi calculer la dérivée de cette dérivée :marteau:
e =/= exponentielle, e est une valeur en mm de même que r

-
ampholyte
- Membre Transcendant
- Messages: 3940
- Enregistré le: 21 Juil 2012, 07:03
-
 par ampholyte » 15 Jan 2013, 10:10
par ampholyte » 15 Jan 2013, 10:10
Bonjour,
Il faut également te souvenir que
})' = u'(x) exp{u(x)})
Donc par déduction :
 + r})' = (cos(wt) + r)' exp{cos(wt) + r} = -w. sin(wt) exp{cos(wt) + r})
PS : fait attention quand tu n'utilises pas les balises TEX de bien mettre les parenthèses où il faut car on aurait pu croire que tu essayais de calculer la dérivée de
.t + r)
-
onizuka1990
- Messages: 4
- Enregistré le: 15 Jan 2013, 09:52
-
 par onizuka1990 » 15 Jan 2013, 10:15
par onizuka1990 » 15 Jan 2013, 10:15
Je m'excuse je vais éditer je viens de me rendre compte d'un truc, e =/= exp, e en fait c'est une valeur en mm.
Voila j'ai édité je pense que c'est plus clair comme ça

-
ampholyte
- Membre Transcendant
- Messages: 3940
- Enregistré le: 21 Juil 2012, 07:03
-
 par ampholyte » 15 Jan 2013, 10:33
par ampholyte » 15 Jan 2013, 10:33
Ta dérivée est correcte, qu'est ce qui te pose problème ?
Pour le calcul de f''(x) il suffit de te rappeler que la dérivée de (sin(wt))' = wcos(wt)
-
onizuka1990
- Messages: 4
- Enregistré le: 15 Jan 2013, 09:52
-
 par onizuka1990 » 15 Jan 2013, 10:45
par onizuka1990 » 15 Jan 2013, 10:45
ampholyte a écrit:Ta dérivée est correcte, qu'est ce qui te pose problème ?
J'ai eu un doute sur la méthode de résolution, ça fait tellement longtemps les dérivées
J'ai posé
 = (u.v)' = uv'+u'v)
Avec

donc

Et
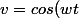)
donc
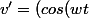)' = - w sin (wt))
Ce qui me donne :
 = u'v+uv' = 0cos(wt) + e(-wsin(wt)) = -ewsin(wt))
Donc tout est correct :we: ?

-
ampholyte
- Membre Transcendant
- Messages: 3940
- Enregistré le: 21 Juil 2012, 07:03
-
 par ampholyte » 15 Jan 2013, 10:52
par ampholyte » 15 Jan 2013, 10:52
C'est juste mais tu as beaucoup plus simple.
x'(t) = (k.u)' = k.u'
avec k = e et u = cos(wt)
d'où x'(t) = e*(-w.sin(wt)) = -ew.sin(wt) tout simplement.
-
onizuka1990
- Messages: 4
- Enregistré le: 15 Jan 2013, 09:52
-
 par onizuka1990 » 15 Jan 2013, 11:00
par onizuka1990 » 15 Jan 2013, 11:00
Ah ouai beaucoup plus simple en effet, un très très grand merci
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 95 invités
