Dérivée de cos ( arc cos x) et arc cos(cos(x))
2 messages
- Page 1 sur 1
dérivée de cos ( arc cos x) et arc cos(cos(x))
par hypathie31415 » 03 Nov 2019, 05:59
je cherche les dérivées de cos(arccos(x)) et de arccos(cos (x)) .quelqu'un peut il m'aider?S'agit -il de g rond f?
Re: dérivée de cos ( arc cos x) et arc cos(cos(x))
par mathelot » 03 Nov 2019, 08:12
Bonjour,
pour-1 <=x <=1 , f(x)=Cos (arccos(x) l=x
f'(x)=1 sur ]-1;1[
g(x)=arccos(cos(x))
g est définie sur R,
-périodique, paire.
On peut l'étudier sur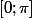
si)=x)
g'(x)=1
si)=-x+2\pi)
(faire un dessin du cercle trigo)
=-1 sur ]\pi,2\pi[)
En dérivant
=- \dfrac{1}{\sqrt{1-cos^2(x)}} * (-sin(x))=\dfrac{sin(x)}{|sin(x)|})
pour-1 <=x <=1 , f(x)=Cos (arccos(x) l=x
f'(x)=1 sur ]-1;1[
g(x)=arccos(cos(x))
g est définie sur R,
On peut l'étudier sur
si
g'(x)=1
si
(faire un dessin du cercle trigo)
En dérivant
2 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 9 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :