Bonjour,
Une question toute bête mais, est-ce qu'une fonction dérivable en un point est toujours différentiable en ce même point ?
Car je comprends pas tellement la différence entre les deux, à partir de quel moment ça diffère, c'est une question que je me suis posé, ça me tracasse :)
Dérivable et différentiable
6 messages
- Page 1 sur 1
Oui bien sur :
Dérivabilité :
une fonction définie un intervalle
définie un intervalle  est dite dérivable en un point
est dite dérivable en un point  de
de  s'il existe un réel l tel que :
s'il existe un réel l tel que :
-f(a)}{h} = l) où l est le nombre dérivée en
où l est le nombre dérivée en  , noté
, noté ) .
.
Différentiabilité :
Soit et
et  deux espaces vectoriels normés.
deux espaces vectoriels normés.
Soit un ouvert de
un ouvert de  et
et  une application.
une application.
On dit que est différentiable en
est différentiable en 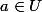 s'il existe une application
s'il existe une application  continue et linéaire de
continue et linéaire de  dans
dans  tel que
tel que
-f(a)-L(h)||_F}{||h||_E} = 0)
On note la différentielle de
la différentielle de  au point
au point  ,
, 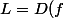_a)
Dérivabilité :
une fonction
Différentiabilité :
Soit
Soit
On dit que
On note
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 280 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
