Application indéfiniment différentiable

[Skullkid]

Bonsoir, j'ai un doute sur la justesse d'un raisonnement :

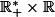
J'ai une fonction de deux variables définie comme somme d'une série sur . On me demande de montrer qu'elle est indéfiniment différentiable et d'exprimer sous la forme d'une somme de série.

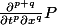
Par des théorèmes de dérivation d'une somme de série, je parviens à , les problèmes surviennent en ce qui concerne la différentiabilité : je dois montrer que est continue pour tous p,q.

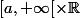
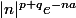
Pour cela, je localise (t,x) dans avec a>0 et je majore par qui est le terme général d'une série convergente indépendante de x et de t. J'en déduis que la dérivée partielle est continue, donc que P est indéfiniment différentiable. C'est sur ce point que j'ai un doute.

Merci d'avance de m'éclairer.

[alavacommejetepousse]

bonsoir

c'est parfaitement correct.

[Skullkid]

Merci beaucoup :)