Bonjour les isometries f qui conservent les angles orientés sont appelé déplacament et celles qui transformes les angles orientés en leur opposés sont les antidéplacement.
1_Soit f# la partie linéaire de f
f étant une isométrie det(f#)=+ou- 1
comment le démontrer simplement?
2_Si det(f#)=1 alors f est un déplacement
comment le démontrer simplement?
3_Si det(f#)=-1 alors f est un antidéplacement
comment le démontrer simplement?
Pour esseyer de repondre au 1 dans le cas du plan j'ai esseyé de prendre une matrice (abcd) et de trouver que |ad-bc|=1 en disant que
(ax+cy)²+(bx+dy)²=x²+y²
je pense qu'il doit y avoir + simple car il on passe au cas de l'espace ça devient horrible!
Merci pour votre aide
Déplacement et antidéplacement
8 messages
- Page 1 sur 1
par yos » 01 Mar 2007, 11:31
Bonjour.
Tout dépend ce qu'on sait au départ.
Si tu parles d'angle orienté, c'est que tu parles d'isométries du plan. Si tu as la classification complète de ces isométries (rotations-translations d'un côté et symétries glissées de l'autre), les matrices des linéaires associées sont immédiates et les déterminants aussi.
Dans l'espace il n'y a pas d'angles orientés. L'orientation se fait par les bases dont on montre qu'elles sont de deux types possibles justement grâce à la notion de déterminant. Ce qui fait que dans l'espace, la question est vide.
Tout dépend ce qu'on sait au départ.
Si tu parles d'angle orienté, c'est que tu parles d'isométries du plan. Si tu as la classification complète de ces isométries (rotations-translations d'un côté et symétries glissées de l'autre), les matrices des linéaires associées sont immédiates et les déterminants aussi.
Dans l'espace il n'y a pas d'angles orientés. L'orientation se fait par les bases dont on montre qu'elles sont de deux types possibles justement grâce à la notion de déterminant. Ce qui fait que dans l'espace, la question est vide.
par manu18ck » 01 Mar 2007, 11:45
merci beaucoup pour ces eclairssissement
dans le cas de l'espace comment montre t-on qu'une isométrie a sa partie linéaire de dterminant egal à +ou-1?
apré promi j'arete de t'embeter lol
dans le cas de l'espace comment montre t-on qu'une isométrie a sa partie linéaire de dterminant egal à +ou-1?
apré promi j'arete de t'embeter lol
par yos » 01 Mar 2007, 12:41
C'est la définition d'un déplacement (en dimension 3 comme en dimension 25, et aussi en dimension 2, sauf au lycée ou le déterminant est pas au programme). Je résume :
1) Orientation de l'espace (toute dimension)
Tu as une relation d'équivalence sur l'ensemble des bases : B R B ' ssi
. Il n'y a que deux classes d'équivalence. En choisir une (qu'on appelle l'ensemble des bases directes), c'est orienter l'espace.
2) On appelle isométries positives celles qui transforme une base directe en une base directe.
3) On appelle déplacement les isométries affines dont l'isométrie linéaire associée est positive.
Tu vois bien qu'il n'y a rien à démontrer sauf dans le cas du plan et si on utilise les définitions du lycée.
1) Orientation de l'espace (toute dimension)
Tu as une relation d'équivalence sur l'ensemble des bases : B R B ' ssi
2) On appelle isométries positives celles qui transforme une base directe en une base directe.
3) On appelle déplacement les isométries affines dont l'isométrie linéaire associée est positive.
Tu vois bien qu'il n'y a rien à démontrer sauf dans le cas du plan et si on utilise les définitions du lycée.
par BQss » 01 Mar 2007, 14:14
Salut,
on peut aussi dire:
La partie lineaire d'une isometrie est un isometrie vectoriel car MN=f(M)f(N) entraine evidemment:
||=||\vec{f(M)f(N)}||=||\vec{MN}||)
Il ne te reste donc plus qu'a prouver qu'une isometrie vectorielle a pour determinant 1 ou -1.
Pour ca tu sais que si une application lineaire conserve les normes elle, conserve le produit scalaire, ca se prouve en trois ligne grace a l'identité de polarisation(il y a meme equivalence).
La matrice A associée dans une base orthonormale, change donc cette base en une base orthonormale(on vient la de definir en fait du meme coup trois definition equivalente d'un endomorphisme orthogonale et l'ensemble de ces matrices associées est appelé groupe orthogonale).
*On en deduit alors que pour cette matrice:
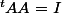
car la norme des vecteurs colonne vaut 1 et leur produit scalaire vaut 0. Ces produit correspondent a la multiplication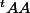
et le resultat vaut donc 1 pour la diagonale et 0 ailleurs.
on a donc=det(I)=1)
soit^2 = det(I) =1)
soit=^+_-1)
avec)
le determinant de A.
*Tout ceci est valable pour n<=3.
on peut aussi dire:
La partie lineaire d'une isometrie est un isometrie vectoriel car MN=f(M)f(N) entraine evidemment:
Il ne te reste donc plus qu'a prouver qu'une isometrie vectorielle a pour determinant 1 ou -1.
Pour ca tu sais que si une application lineaire conserve les normes elle, conserve le produit scalaire, ca se prouve en trois ligne grace a l'identité de polarisation(il y a meme equivalence).
La matrice A associée dans une base orthonormale, change donc cette base en une base orthonormale(on vient la de definir en fait du meme coup trois definition equivalente d'un endomorphisme orthogonale et l'ensemble de ces matrices associées est appelé groupe orthogonale).
*On en deduit alors que pour cette matrice:
car la norme des vecteurs colonne vaut 1 et leur produit scalaire vaut 0. Ces produit correspondent a la multiplication
on a donc
soit
soit
avec
*Tout ceci est valable pour n<=3.
par BQss » 01 Mar 2007, 14:44
Ensuite pour le plan par exemple tu as donc:
avec une matrice
(a c
b d)
a^2+b^2=1
c^2+d^2=1
il existe alors w et z tel que:
a=cos(z) b=sin(z)
c=cos(w) d=sin(w)
et
det(A)=ad-bc=sin(w-z)= +1 ou -1
donc w-z=+Pi/2 ou - Pi/2
donc pour w=z+Pi/2(det=1) tu as:
(cosz -sinz
(sinz cosz)
qui definie la matrice associée a une rotation d'angle z
pour w=z-Pi/2(det=-1) tu as:
(cosz sinz
(sinz -cosz)
qui definie la matrice associée a une reflexion d'axe delta avec (e1,delta)=z/2 ou e1 est le vecteur de la base canonique associé a la premiere coordonnée.
avec une matrice
(a c
b d)
a^2+b^2=1
c^2+d^2=1
il existe alors w et z tel que:
a=cos(z) b=sin(z)
c=cos(w) d=sin(w)
et
det(A)=ad-bc=sin(w-z)= +1 ou -1
donc w-z=+Pi/2 ou - Pi/2
donc pour w=z+Pi/2(det=1) tu as:
(cosz -sinz
(sinz cosz)
qui definie la matrice associée a une rotation d'angle z
pour w=z-Pi/2(det=-1) tu as:
(cosz sinz
(sinz -cosz)
qui definie la matrice associée a une reflexion d'axe delta avec (e1,delta)=z/2 ou e1 est le vecteur de la base canonique associé a la premiere coordonnée.
par yos » 01 Mar 2007, 18:12
Ah oui j'ai pas répondu à la première question. Je pense que BQSS s'en est chargé. Sinon, la condition "isométrie" se traduit par une matrice A telle que 
. On prend le déterminant des deux côtés et on utilise le fait que A et 
ont même déterminant.
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 24 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :