Démonstration th de Wilson

[NICO 97]

Bonjour,
Je regarde la démonstration du th de Wilson, et je bloque.

On arrive à montrer que si p est premier, alors ,
pour tout m entier,
m²=1[p] ssi m=1[p] ou m=(1-p)[p]

Il nous est alors possible de regrouper chaque facteur de N= (p-2)! Avec son inverse modulo p de manière à monter que N=1[p]

Mais je n'arrive à faire ce regroupement

Si quelqu'un pouvait me montrer, d'avance merci.

[abcd22]

Bonjour,

m²=1[p] ssi m=1[p] ou m=(1-p)[p]

C'est ssi m = 1 [p] ou m = -1 = p - 1 [p].

Il nous est alors possible de regrouper chaque facteur de N= (p-2)! Avec son inverse modulo p de manière à monter que N=1[p]

C'est (p - 1)!. Si p est premier, Z/pZ est un corps, donc 1, 2, ..., p - 1 sont inversibles modulo p. Les inverses sont forcément aussi une des classes de 1, 2, ..., p - 1 modulo p, pour un i avec 1 i p - 1, on a deux possibilités :
– l'inverse de la classe de i n'est pas la classe de i : on regroupe i et son inverse, le produit fait 1, ils sont éliminés du produit ;
– l'inverse de la classe de i est la classe de i : on ne peut pas éliminer i du produit.
On obtient que modulo p, (p - 1)! est égale au produit des éléments de /n;) qui sont leur propre inverse, autrement dit les solutions de m² = 1 [p].

[mathelot]

salut,




soit un entier premier.
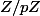est un corps.
l'équation d'inconnue m
s'écrit:

dans un corps , il n'y a pas de diviseur de zéro.
Donc il y a exactement deux classes qui vérifient cette équation: 1 et (p-1).

mais cette équation s'écrit aussi
donc dans les (p-1) classes inversibles, il y en a exactement 2 qui sont
égales à leurs inverses et les autres sont différentes de leurs inverses.

d'ou:
les autres produits se sont simplifiés deux à deux.

[NICO 97]

d'ou:
les autres produits se sont simplifiés deux à deux.

Merci, mais en fait c'est ça que je ne vois pas, le "deux à deux"
Avez vous un exemple?

[NICO 97]

A, c'est bon, je viens de comprendre vos posts, merci beaucoup! :we:

[leon1789]

Avez vous un exemple?

tu n'as qu'à prendre p=13 et voir par toi-même. C'est un bon petit exercice pour savoir si on a compris pourquoi Z/pZ est un corps...