Je n'arrive pas à démontrer l'inégalité suivante
a/b+c + b/c+a + c/a+b > ou = 3/2
Démonstration d'inégalité
10 messages
- Page 1 sur 1
Salut !
Quelles sont les contraintes sur ?
?
Si je prends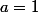 ,
,  et
et 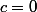 , j'obtiens
, j'obtiens  .
.
Quelles sont les contraintes sur
Si je prends
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Ok, donc  sont trois réels strictement positifs.
sont trois réels strictement positifs.
Déjà, on peux supposer, sans perte de généralité, que .
.
Commence déjà par tout mettre sous le même dénominateur mais sans développer le numérateur et de le dénominateur.
Ensuite, minore le dénominateur puis majore le dénominateur à partir de .
.
:+++:
Déjà, on peux supposer, sans perte de généralité, que
Commence déjà par tout mettre sous le même dénominateur mais sans développer le numérateur et de le dénominateur.
Ensuite, minore le dénominateur puis majore le dénominateur à partir de
:+++:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
En fait, pour montrer cette inégalité (pas facile), il faut savoir déjà ce que tu sais (inégalité de Cauchy, théorèmes de réarrangement, etc...).
Comme je ne sais pas ce que tu sais, je te conseille de regarder sur internet, cherche inégalité de Nesbitt :+++:
Comme je ne sais pas ce que tu sais, je te conseille de regarder sur internet, cherche inégalité de Nesbitt :+++:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
J'ai l'impression que tu bloques un peu. Comme ça peut ne pas paraître évident, je te donne une idée.
1/ Le dénominateur sera(b+c)(a+c)) .
.
Cherchons à le minorer (puisque par passage à l'inverse, on changera l'inégalité). Par hypothèse et
et  donc :
donc :
 ,
,
 ,
,
 .
.
Ainsi(b+c)(a+c)\le ???) .
.
Déduis-en alors(b+c)(a+c)}\ge ???) .
.
2/ Ensuite pour le numérateur, tu as(a+c)+b(b+c)(a+b)+c(b+c)(c+a)) .
.
Ici on majore : par hypothèse, et
et 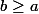 donc :
donc :
(a+c)\ge ???) ,
,
(a+b)\ge ???) ,
,
(c+a) \ge ???) .
.
Ainsi(a+c)+b(b+c)(a+b)+c(b+c)(c+a)\ge ???) .
.
3/ Déduis-en alors(a+c)+b(b+c)(a+b)+c(b+c)(c+a)}{(a+b)(b+c)(a+c)}\ge ???) .
.
:we:
1/ Le dénominateur sera
Cherchons à le minorer (puisque par passage à l'inverse, on changera l'inégalité). Par hypothèse
Ainsi
Déduis-en alors
2/ Ensuite pour le numérateur, tu as
Ici on majore : par hypothèse,
Ainsi
3/ Déduis-en alors
:we:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
En fait, pour montrer cette inégalité (pas facile), il faut savoir déjà ce que tu sais (inégalité de Cauchy, théorèmes de réarrangement, etc...).
Comme je ne sais pas ce que tu sais, je te conseille de regarder sur internet, cherche "inégalité de Nesbitt"
:we:
Comme je ne sais pas ce que tu sais, je te conseille de regarder sur internet, cherche "inégalité de Nesbitt"
:we:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 25 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
