Démonstration de l'inégalité arithmetico-geometrique

[tcdovdi14]

Bonjour,

Je suis en MPSI, on a pas encore commencé le programme de maths et on a cet exo a faire :

Soit vérifiant pour tout : . On veut prouver :



Voilà les questions où je bloque :
1) Montrer le résultat dans le cas où (k entier).
Là je suis parti sur une récurrence mais ça bloque a l'hérédité
2) Montrer que si le résultat est vrai au rang n+1, alors il est vrai au rang n
3) conclure

Le but de l'exos est de montrer l'inégalité arithmetico-geometrique après.

Merci !

[pascal16]

soit
x= x1+...+xn
et y = xn+1.....x2n
on a
f((x+y)/2) ≤f(x+y) / 2
f((x1+...+xn + xn+1.....x2n)/2 ) ≤ (f(x1+ ..+xn) + f(xn+1.....x2n)) /2

[tcdovdi14]

Merci de votre réponse.

J'étais arrivé jusque là, mais c'est le passage de f(x1+...+xn)+f(x(n+1)+...+x2n) à f(x1) + ... + f(x2n) où je bloque. Ne connaissant pas la fonction, je ne sait pas comment la decomposer, ou montrer que la second partie est supérieure à la première

[pascal16]

ici n= 2^(k+1)
f((x1+...+xn + xn+1.....x2n)/2 ) ≤ (f(x1+ ..+xn) + f(xn+1.....x2n)) /2

par HR pour n= 2^k
f(x1+ ..+xn) ≤ (f(x1)+...... +f(xn)) /2^k
f(xn+1.....x2n)) ≤ ( f(xn+1)+...... +f(x2n)) /2^k

f((x1+...+xn + xn+1.....x2n)/2 ) ≤( (f(x1)+...... +f(xn)) /2^k + ( f(xn+1)+...... +f(x2n)) /2^k )) /2
≤( ( la somme de tout / 2^k)) /2
≤ la somme de tout / 2^k+1
≤ la somme de tout / (n+1)

[Kolis]

Bonsoir !
Pour le cas où je te laisse le soin de déchiffrer ce que te dit @pascal16.

Pour la démonstration de la relation pour quand elle est vraie pour :
Soit .
On pose

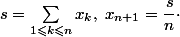
Alors
Donc et puisque il vient


qui n'est autre que l'inégalité cherchée pour .

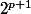
Pour finir, en prenant puisque la relation est vraie pour , en vertu de la propriété précédente elle sera vraie aussi pour

[tcdovdi14]

Merci pour vos retours !

Après, il nous est demandé de démontrer l'inégalité arithmético-géométrique, à savoir :


En utilisant ce que l'on a montré précédemment, il suffirait de trouver une fonction , telle que ou bien avec . On retomberait directement sur la formule démontrée plus haut. Le hic est que je ne sais pas comment formulée cette fonction, peut-être que la formule que je viens de donner suffit ? J'ai fais des recherche avec , ...etc. mais à chaque fois qu"une des formules marche pour un côté, ça ne marche pas de l'autre !

Merci

[Ben314]

Salut,
Si on pose (ce qu'on peut faire vu que les sont >0) alors l'inégalité elle s'écrit comment en terme de ?

[Tuturrrrrr258]

Bonsoir !
Pour le cas où je te laisse le soin de déchiffrer ce que te dit @pascal16.

Pour la démonstration de la relation pour quand elle est vraie pour :
Soit .
On pose

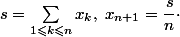
Alors
Donc et puisque il vient


qui n'est autre que l'inégalité cherchée pour .

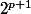
Pour finir, en prenant puisque la relation est vraie pour , en vertu de la propriété précédente elle sera vraie aussi pour

Bonjour, je viens vers vous pour vous demander pourquoi on a le droit de poser xn=s/n. Puisque nous devons obtenir une propriété vraie pour tout xn. Je ne sais pas si j’ai été clair. Merci d’avance.

[Kolis]

Tu veux une formule pour donc à partir d'une famille !
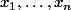
Rien ne t'interdit d'introduire un qui t'arrange puis d'appliquer la formule connue pour