Définition au voisinage de xo

par **Mathusalem** » 20 Nov 2009, 19:29

Bonsoir,

J'ai la définition suivante dans mon cours :

Soit

une fonction et soit

. On dit que f est définie au voisinage de

s'il existe

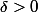
tel que

.

On me donne comme exemple :
D =

, f(x) = x, x

Ici, f n'est définie au voisinage d'aucun points.

Je ne comprends pas pourquoi f n'est définie au voisinage d'aucun point. Prenons un point x0 irrationnel. Il existe

> 0 tel que l'intervalle

soit inclus dans D union {x0}. Il me semble qu'au voisinage de tout irrationnel il existe un rationnel. Donc en principe il doit exister un delta qui me prend les deux rationnels entourant le x0 irrationnel.
Peut-être que j'ai tout faux conceptuellement, dans lequel cas, un éclaircissement serait le bienvenu

A+

par **barbu23** » 20 Nov 2009, 19:37

Parceque si tu prends un point

aucun intervalle contenant

:

n'est inclus dans

qui est

! :happy3:

par **Mathusalem** » 20 Nov 2009, 19:41

Je viens de lâcher un gros "Aaaaaaaaaaaaaaaaaah mais oui".

Donc merci bien :)

A+

par **alavacommejetepousse** » 20 Nov 2009, 19:55

bonsoir

en toute rigueur x0 doit être élément de D
ex
f définie sur R* par f(x) = 1/x n 'est pas définie au voisinge de 0 et pourtant avec ta définition elle l'est

par **Mathusalem** » 20 Nov 2009, 20:08

Bonsoir,

Posons x0 = 0 et soit d > 0 quelconque.
On a bien ]-d, +d[ inclu dans R, ainsi, f est définie au voisinage de x0 = 0

Selon moi, 1/x ainsi posée est définie au voisinage de x0.

par **barbu23** » 20 Nov 2009, 20:13

Non, seulement

qui est inclus dans le domaine de definition de

par contre

non ! :happy3:
Car le domaine de définition de

est

Cordialement ! :happy3:

par **Mathusalem** » 20 Nov 2009, 20:18

barbu23 a écrit:Non, seulement qui est inclus dans le domaine de definition de par contre non ! :happy3:
Car le domaine de définition de est
Cordialement ! :happy3:

Oui, seulement, la définition dit, que l'intervalle doit être inclu dans le domaine union x0. Du coup, selon moi, et même selon mon cours, f définit sur R*, 1/x, est définit au voisinage de zéro.

A+

par **alavacommejetepousse** » 20 Nov 2009, 20:21

oui alors qu elle ne devrait pas

par **Mathusalem** » 20 Nov 2009, 20:22

Mais en réfléchissant de manière pragmatique, comment peut-on affirmer que 1/x n'est pas définie au voisinage de 0 ? Elle n'est pas définie en zéro, mais partout ailleurs, si.

. . . :hum:

par **barbu23** » 20 Nov 2009, 20:24

Non

est la même chose que écrire :

:happy3:

par **alavacommejetepousse** » 20 Nov 2009, 20:26

Mathusalem a écrit:Mais en réfléchissant de manière pragmatique, comment peut-on affirmer que 1/x n'est pas définie au voisinage de 0 ? Elle n'est pas définie en zéro, mais partout ailleurs, si.

. . . :hum:

bon

un voisinage d un point doit contenir ce point c est comme ça en topologie

par **barbu23** » 20 Nov 2009, 20:26

Mathusalem a écrit:Mais en réfléchissant de manière pragmatique, comment peut-on affirmer que 1/x n'est pas définie au voisinage de 0 ? Elle n'est pas définie en zéro, mais partout ailleurs, si.

. . . :hum:

Non, elle est définie au voisinage de

, mais pas en

! et

est un de ses voisinages avec

! :happy3:

par **Ben314** » 20 Nov 2009, 20:27

Il est EXTREMENT utile de pouvoir dire que le fonction x->1/x est définie au voisinage de 0 :
parmi les deux phrases suivantes :
"Quelle est la limite de 1/x lorsque x tend vers 0"
"Quelle est la limite de racine(x) lorsque x tend vers -1"
1) Chercher l'erreur.
2) Expliquez...

par **Ben314** » 20 Nov 2009, 20:30

En topologie (générale) il est parfaitement vrai que (par définition) le voisinage d'un point DOIT contenir le point, MAIS, lorsque l'on dit qu'une fonction est définie au voisinage d'un point cela signifie dans un voisinage "pointé" c'est à dire sur un voisinage privé du point.

par **alavacommejetepousse** » 20 Nov 2009, 20:31

Ben314 a écrit:Il est EXTREMENT utile de pouvoir dire que le fonction x->1/x est définie au voisinage de 0 :
parmi les deux phrases suivantes :
"Quelle est la limite de 1/x lorsque x tend vers 0"
"Quelle est la limite de racine(x) lorsque x tend vers -1"
1) Chercher l'erreur.
2) Expliquez...

il est EXTREMEMENT faux de dire qu elle l est
pour chercher la limite en un point il faut et suffit que ce point soit adhérent à l ensemble de définition ce qui est le cas ici

par **Ben314** » 20 Nov 2009, 20:36

Je te parie que cette définition va servir au prof pour définir les limites des fonctions réelles.
A mon avis, il ne veut pas définir la notion de "point adhérent" vu son objectif d'enseignement et/ou le niveau ou se situe le cours.

par **Ben314** » 20 Nov 2009, 20:40

Je te rappelle (?) aussi qu'une définition est... une définition :
Celon les ouvrages, un anneau peut soit désigner un anneau uniataire comutatif intégre, soit rien de tout cela. Un compact peu être ou ne pas être séparé (celon que l'auteur a ou pas des affinitées anglosaxonnes)...

Tu N'AS PAS a dire qu'une DEFINITION est fausse.

par **Mathusalem** » 20 Nov 2009, 23:50

Et bien merci pour ces précisions :

C'est la définition que j'ai dans le livre (celle donnée auparavant). De plus, le point adhérant a aussi été défini. Mon prof de mathématiques étant très pointilleux, je doute qu'il se soit trompé lorsqu'il disait que 1/x est defini au voisinage de 0. Comme ben l'a dit, le malentendu doit venir du fait que plusieurs définitions sont possibles.

Merci encore,

Bonne soirée

par **alavacommejetepousse** » 21 Nov 2009, 13:08

je ne vais pas argumenter à l infini mais un voisinage d'un point est une notion précise , si on veut retirer le point on parle de voisinage épointé, mais si c'est pour raconter n'importe quoi sur les voisinages mieux vaut ne pas en parler

Définition au voisinage de xo

Définition au voisinage de xo

Qui est en ligne