Définition de exp, cos et sin

[L.A.]

Bonjour à tous.

La fonction exponentielle est définie par la série entière
exp(x) = (Somme de k=0 à inf) x^k/k!

a partir de là, on peut montrer exp(a+b) = exp(a)exp(b) par un produit de Cauchy.

de même les fonctions cosinus et sinus sont défines comme parties réelle et imaginaire de exp(ix)
elles sont 2pi périodiques, comprises entre -1 et 1, enfin a ce qu'on dit...

Mais peut-on montrer directement ces propriétés à partir de la série entière ?
|exp(ix)|=1 ? exp(i2pi)=1 ?

[skilveg]

En fait, quand on procède dans cet ordre, on définit comme la moitié du générateur positif du sous-groupe de des tels que (i.e. le noyau de . Ce noyau est fermé, donc est , ou de la forme 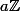; ce n'est pas car l'exponentielle est surjective dans 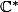, ni car il existe avec (en particulier 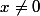), et avec ).

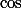Ce n'est qu'ensuite que l'on vérifie la -périodicité de et 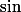(et on a de toute façon l'identité ).

J'espère que ça répond à ta question...