Définition application linéaire coïncidente

[Leia73]

Bonjour,

Au détour d'un corrigé de sujet de Concours, je suis tombé sur l'énoncé suivant :
f et g coïncident sur la base B donc elles sont égales.

Malgré des recherches, je n'arrive pas à trouver de définition concrète de la coïncidence de deux applications linéaires.
Pourriez-vous m'éclairer ?

[zwijndrecht]

Bonjour,

Cela signifie simplement que les deux applications linéaires sont égales sur tous les vecteurs de la base .
L'égalité des deux applications linéaires se déduit alors par linéarité.

Si est le -espace vecroriel de départ et si 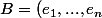, l'hypothèse signifie juste que ,
Tout vecteur s'écrit , avec .
On a alors, par linéarité,