Défi analytique

[Imod]

Bonsoir,
On n'a pas besoin d'utiliser le fait que les VA forment un segment, il suffit, comme le dit Flodelarab de montrer que la continuité permet de créer une barrière entre deux VA, barrière qui devient un puits

Là tu m'intéresses alben comment creuses-tu ton puits ?

Imod

[muse]

On pourraiessayer par l'absurde non ?

A chaque fois que on demonter que une suite converageait c'était pas l'absurde.

[alben]

Je t'ai répondu par message privé afin de permettre à ceux qui veulent chercher de le faire.
PS j'ai un peu cafouillé dans les messages privés :cyborg:

edit : @Rain' : tu peux rendre la pelle que tu as volé à ta petite soeur, c'est un puits sans fond et elle en a besoin pour ses pâtés de sable

[Imod]

Je me permets de préciser un peu l'indication d'alben ( qu'il me réprimande s'il estime que j'ai outrepassé mes droits ) . La suite a au moins une valeur d'adhérence , si elle en avait deux ( comme ... :hum: ... je m'égare ) alors sur et la suite est simple . Donc , pourquoi sur ?

Imod

[alben]

Il semble que ce defi n'ai plus de clients. Si c'est le cas, je me propose de poster la réponse envoyée par MP, mais en plus claire de manière à faciliter le travail de Joker, notre chroniqueur officiel

[Imod]

Il semble que ce defi n'ai plus de clients. Si c'est le cas, je me propose de poster la réponse envoyée par MP, mais en plus claire de manière à faciliter le travail de Joker, notre chroniqueur officiel

Je crois en effet que tu peux donner ta solution :we:

Imod

[Nightmare]

Salut Imod:

Ca converge vers un truc du type où f est une fonction dont l'ensemble des zéros est d'intérieur vide.

Non?

[alben]

C'est quoi ta fonction g Nightmare ?

On se donne une fonction continue de [0;1] dans [0;1] et dans [0;1] . est définie par son premier terme et par la relation de récurrence : .
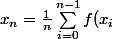Montrer que est convergente .

Préambule : On vérifie facilement que la suite reste à l'intérieur de [0,1]. Elle a au moins une valeur d'adhérence (compacité)
la relation de définition de la suite peut s'écrire
D'où on tire deux observations[list=1]
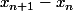
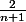
[*]La suite est majorée par , elle tend vers 0
[*] sont du même coté de
[TEX]f(x_n)0 tel que [TEX]x\in ]c-r_1,c+r_1[\Rightarrow f(x)c, cela inverserait simplement le sens de passage de la diode.
Donc f(c)=c
Le puits
Le point c était quelconque, donc tous les points intérieurs à [a,b] sont des points fixes de f. La suite va donc nécessairement atteindre un de ces points puisqu'elle doit aller de a vers b et que son pas tend vers zéro.
Dès que l'un de ces points est atteint, la suite devient constante et a et b ne peuvent être valeurs d'adhérence.
Conclusion l'intérieur de [a,b] est vide et il n'y a qu'une seule valeur d'adhérence qui est donc une limite.

[Imod]

Je ne vois pas ce que représente ta fonction ! Si a un unique point fixe alors converge vers , sinon ça dépend de .

Imod

[Nightmare]

Pardon, c'était g qui était une fonction dont l'ensemble des zéros est à intérieur nul.

On montre facilement qu'il existe une unique subdivision de [0,1], telle que :
pour tout i de [|1;n|]

On note et

f est continue sur [0;1].
On pose :


Sn est une somme de Riemann relativement à foG^-1, fonction continue sur [0:A].

La suite (Sn) converge vers ie vers

Conclusion

[Imod]

J'ai du mal à voir le rapport avec l'exercice proposé , les sont calculés de proche en proche à partir des images par des termes précédents . D'autre part je ne vois pas bien comment on peut avoir unicité des valeurs et de ?

Imod

[Nightmare]

D'accord, j'ai très mal lu l'énoncé, autant pour moi!