Décomposition isométries en symétrie(s) orthogonales

[REGBEL]

Bonjour à tous,

Je suis futur prof de math, et je fais un travail sur la décomposition des isométries en symétrie(s) orthogonales.

En géométrie euclidienne je n'ai pas eu de problème particulier.

Par contre, je voudrais essayer d'aller plus loin et de voir si cette propriété peut se généraliser aux isométries vues comme des endomorphismes du plan, et si oui comment ?

Je n'ai pas trouvé en cherchant sur internet, alors je vous soumets la question !

Merci beaucoup pour vos réponses !!

[Ben314]

Salut,
Je comprend pas franchement la question...
Normalement, dans tout bouquin/site parlant de ce truc là, tu va trouver que :

1) Si E est un espace vectoriel Euclidien de dimension n alors tout élément f du groupe orthogonal O(E) se décompose en au plus n symétries orthogonales par rapport à des hyperplans vectoriels de E.

2) Si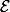 est un espace affine Euclidien de dimension n alors tout élément f du groupe des isométries Is(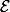) se décompose en au plus n+1 symétries orthogonales par rapport à des hyperplans affines de .

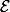Dans les deux cas, la preuve est la même est se fait bêtement en composant (à gauche) f par la symétrie orthogonale par rapport à l'hyperplan médiateur de x et f(x) où x est un vecteur/point tel que f(x) soit différent de x.
On montre aisément que cela fait augmenter d'au moins 1 la dimension du sous espace vectoriel/affine des points fixes de f et donc qu'au bout d'un certain nombre d'étapes on aura f=Id.

[REGBEL]

Bonjour,
Merci beaucoup pour la réponse. Ce n'est pas aussi simple que ça pour moi (je ne fais que commencer à voir toutes ces notions), mais je pense que ça répond à ma question...

[Ben314]

Je peut te détailler la preuve dans le cas affine si tu veut :

Le premier truc à montrer c'est que l'ensemble des points fixe d'une application affine est, s'il n'est pas vide un sous-espace affine de :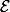
On suppose donc qu'il n'est pas vide et on prend . Pour tout point on a alors
(car )
où 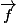est l'application linéaire associée à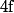
qui est un s.e.v. de E.
Donc qui est bien un sous espace affine de .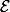

Remarque : peut être vide : c'est par exemple clairement le cas si 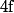est une translation de vecteur non nul (qui est non seulement une application affine, mais même une isométrie)

Considérons maintenant une isométri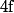e de .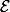
Si il n'y a rien à démontrer (elle est la composée de zéro symétrie orthogonale par rapport à des hyperplans).
Sinon, il existe au moins un point tel que .
On note l'hyperplan médiateur du segment c'est à dire l'hyperplan passant par le milieu de et de vecteur normal qui est aussi l'ensemble des points tels que .
On note aussi la symétrie orthogonale par rapport à cet hyperplan. Par construction, échange 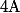et donc c'est à dire .
D'un autre coté, si alors donc vu que 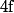est une isométrie. Cela prouve que donc que c'est à dire que .

Bilan : mais (car mais )
Donc, si est vide alors est un sous espace affine (donc de dimension au moins 0) et, si est un s.e.a. de dimension alors est un sous espace affine de dimension au moins .
Si (c'est à dire si ), on réitère le procédé en partant de 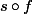de façon à de nouveau augmenter la dimension de l'ensemble des points fixes.
Au bout d'un certain nombre étapes, on aura donc où les sont des symétries orthogonales par rapport à des hyperplans, donc vérifient en particulier ce qui prouve que .

Remarques :
1) La preuve est exactement la même dans le cas vectoriel sauf que, l'ensemble des "vecteurs fixes" de f est toujours un s.e.v. de E (il ne peut pas être vide) donc le nombre d'étapes est majoré par n et pas par n+1.
2) La preuve est non seulement très simple, mais elle donne explicitement un algorithme de construction de symétries orthogonales dont la composée donne f et on peut parfaitement suivre cet algorithme pour trouver comment décomposer une isométrie donnée (essaye de le faire par exemple pour une translation du plan)
3) Le théorème en question permet aussi de "classer" les isométries (affines ou vectorielles) en fonction du nombre de symétries orthogonales qu'il faut pour les décomposer. Par exemple, en dimension 3 on a :
0 symétries orthogonales par rapport à des plans => Id
1 symétries orthogonales par rapport à des plans => Symétrie orthogonale
2 symétries orthogonales par rapport à des plans => Translation si les 2 plans sont parallèles et rotation autours de la droite intersection des deux plans sinon.
3 symétries orthogonales par rapport à des plans => Symétrie glissée (= composée d'une symétrie par rapport à un plan et d'une translation de vecteur "parallèle" au plan) ou bien composée d'une rotation suivant une droite et d'une symétrie par rapport à un plan orthogonal à la droite (avec comme cas particulier les symétries centrales si la rotation est un demi tour)
4 symétries orthogonales par rapport à des plans => Vissage (= composée d'une rotation par rapport à une droite et d'une translation de vecteur "parallèle" à la droite)

[REGBEL]

Ca y est, j'ai compris !!

Merci beaucoup pour cette réponse.