[MPSI] Bloqué sur les projections orthogonales...
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
 par pouik » 26 Mai 2007, 07:29
par pouik » 26 Mai 2007, 07:29
Bonjour,
Pourriez vous m'aider à résoudre ces deux questions auxquelles je ne comprends absolument rien !! Merci d'avance.
Soient

un espace euclidien,

, et

. On suppose
)
libre, et on note
)
.
1. Montrer que pour tout projecteur orthogonal

de

,
|x) = ||x - p(x)||^2)
.
2. Etablir, pour tout

, l'égalité :
 = d(x,F)^2 g(x_1, ..., x_p))
(on effectuera des opérations élémentaires sur le déterminant d'ordre
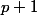
).

-
nuage
- Membre Complexe
- Messages: 2214
- Enregistré le: 09 Fév 2006, 22:39
-
 par nuage » 26 Mai 2007, 08:35
par nuage » 26 Mai 2007, 08:35
Salut,
Il y a sans doute une erreur dans la question 1. Je ne vois pas le sens de l'opération
|x)
que je lis comme la dfférence entre une vecteur est un scalaire.
Il s'agit sans doute de montrer
|x = ||x - p(x)||^2)
Dans ce cas on peut développer
)^2)
en utilisant
)|p(x)=0)
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 26 Mai 2007, 08:47
par yos » 26 Mai 2007, 08:47
nuage a écrit:Salut,
Il y a sans doute une erreur dans la question 1. Je ne vois pas le sens de l'opération
|x)
Bof. Comme ambiguité j'ai connu pire.
-
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
 par pouik » 26 Mai 2007, 08:54
par pouik » 26 Mai 2007, 08:54
[quote="pouik"]
1. Montrer que pour tout projecteur orthogonal

de

,
|x) = ||x - p(x)||^2)
.
QUOTE]
En fait c'est le produit scalaire de
)
avec

. Non ? :hum:
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 26 Mai 2007, 08:59
par yos » 26 Mai 2007, 08:59
pouikEn fait c'est le produit scalaire de [TEX a écrit:x - p(x)[/TEX] avec

. Non ?
Si tu n'en est pas certain, c'est que nuage avait raison : c'est ambigu.
-
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
 par pouik » 26 Mai 2007, 09:18
par pouik » 26 Mai 2007, 09:18
Non je suis certain de ce qui est écrit sur mon ennoncé et donc c'es effectivement ce que j'ai dit! sur de sur !!!

-
nuage
- Membre Complexe
- Messages: 2214
- Enregistré le: 09 Fév 2006, 22:39
-
 par nuage » 26 Mai 2007, 14:40
par nuage » 26 Mai 2007, 14:40
Salut,
je reviens un peu tard.
Juste une remarque pour
pouik : pour écrire ce que tu veux il faut bien placer les parenthèses
)|x)
et mon indication précédente reste valable. j'ai juste développé le produit.
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 26 Mai 2007, 14:52
par aviateurpilot » 26 Mai 2007, 14:52
salut les amis,
c'est quoi
\ et\ g(y_1,y_2,..,y_p))
.??
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 26 Mai 2007, 15:21
par aviateurpilot » 26 Mai 2007, 15:21
pouik a écrit:Bonjour,
Pourriez vous m'aider à résoudre ces deux questions auxquelles je ne comprends absolument rien !! Merci d'avance.
Soient

un espace euclidien,

, et

. On suppose
)
libre, et on note
)
.
1. Montrer que pour tout projecteur orthogonal

de

,
|x) = ||x - p(x)||^2)
.
2. Etablir, pour tout

, l'égalité :
 = d(x,F)^2 g(x_1, ..., x_p))
(on effectuera des opérations élémentaires sur le déterminant d'ordre
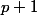
).
1. comme nuage a dit
2. je ne sais pas que veux tu dire par
)
mais je vais montrer un resultat semblable,
soit

,et

la projection orthogonal sur
.
\in F\Rightarrow \exist (a_i)_{i=1..n}\ tel\ que\ x-p(x)=\bigsum_{i=1}^{n}a_ix_i)
soit
=det(Mat_{B}(y_1,...,y_n)))
avec

base orthonormé direct de
)
=f(x-\bigsum_{i=1}^{n}a_ix_i,x_1,..,x_p)=f(x-p(x),x_1,..,x_p)=det( mat_{(B)}(x-p(x),x_1,..,x_p) ))
tel que
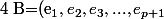)
,
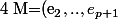)
base orthonormé direct de
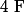
et
}{||x-p(x)||},)
donc
=det (mat_{B}(x-p(x),x_1,..,x_p) )=det( Mat_{(e_1)}(x-p(x) )).det( Mat_{(M)}(x_1,..,x_p))=||x-p(x)||.f(x_1,...,x_n))
et
||=d(x,F))
-
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
 par pouik » 26 Mai 2007, 16:05
par pouik » 26 Mai 2007, 16:05
aviateurpilot a écrit:1. comme nuage a dit
2. je ne sais pas que veux tu dire par
)
mais je vais
Désolé, on appelle matrice de gram de
)
et on note
)
la matrice (carrée d'ordre

) de terme général
)
.
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 26 Mai 2007, 16:21
par aviateurpilot » 26 Mai 2007, 16:21
pouik a écrit:Désolé, on appelle matrice de gram de
)
et on note
)
la matrice (carrée d'ordre

) de terme général
)
.
merci
je voi qu'il est clair que
_{i,j}=A.T_A)
avec
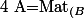}(x,x_1,..,x_p).)
donc
=det(A)^2=f(x,x_1,..x_p)^2)
et donc
=f(x,x_1,..x_p)^2=||x-p(x)||^2f(x_1,..,x_2)^2=d(x,F)^2g(x_1,..,x_p))
-
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
 par pouik » 26 Mai 2007, 16:34
par pouik » 26 Mai 2007, 16:34
Merci,
mais pourriez vous m'expliquer un peu plus en détails comment faire la question 1., je ne comprends pas très bien.
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 26 Mai 2007, 16:38
par aviateurpilot » 26 Mai 2007, 16:38
||^2=(x-p(x)|x-p(x))=(x-p(x)|x)-(x-p(x)|p(x)))
et on a
\in Im(P))
et
\in Ker(p))
car
)=p(x)-pop(x)=p(x)-p(x)=0)
donc
|x)=0)
puisque
)
et
)
sont orthogonal
d'ou
||^2=(x-p(x)|x)-(x-p(x)|p(x))=(x-p(x)|x))
-
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
 par pouik » 26 Mai 2007, 17:17
par pouik » 26 Mai 2007, 17:17
Merci beaucoup, j'ai compris pour la 1.
-
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
 par pouik » 27 Mai 2007, 10:25
par pouik » 27 Mai 2007, 10:25
Bonjour,
pour la 2., je ne comprends pas ces égalités :
aviateurpilot a écrit:1. comme nuage a dit
2. je ne sais pas que veux tu dire par
)
mais je vais montrer un resultat semblable,
soit

,et

la projection orthogonal sur
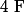
.
\in F\Rightarrow \exist (a_i)_{i=1..n}\ tel\ que\ x-p(x)=\bigsum_{i=1}^{n}a_ix_i)
soit
=det(Mat_{B}(y_1,...,y_n)))
avec

base orthonormé direct de
)
=f(x-\bigsum_{i=1}^{n}a_ix_i,x_1,..,x_p)=G(x-p(x),x_1,..,x_p)=det mat_{(B)}(x-p(x),x_1,..,x_p))
Merci d'avance pour vos explications. :++:
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 27 Mai 2007, 11:35
par aviateurpilot » 27 Mai 2007, 11:35
une petite erreur a écrit:=f(x-\bigsum_{i=1}^{n}a_ix_i,x_1,..,x_p)=\fbox{G(x-p(x),x_1,..,x_p)}=det( mat_{(B)}(x-p(x),x_1,..,x_p) ))
j'ai voulu ecrire ça:
=f(x-\bigsum_{i=1}^{n}a_ix_i,x_1,..,x_p)=\fbox{f(x-p(x),x_1,..,x_p)}=det( mat_{(B)}(x-p(x),x_1,..,x_p) ))
1)
=f(x-\bigsum_{i=1}^{n}a_ix_i,x_1,..,x_p))
là c'est clair puisque j'ai fait des operation elementaire sur la colone de

.
2)
=f(x-p(x),x_1,..,x_p))
ici on j'ai remplacer
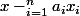
par
.)
3)
,x_1,..,x_p)=det( mat_{(B)}(x-p(x),x_1,..,x_p) ))
ici, par definition puisque
)
est le determinant de la famille libre
)
par rapporta une base orthonermé direct de
)
alors j'ai pris
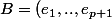)
avec
}{||x-p(x)||})
( et là ob peux supposer que
\neq 0)
sinon
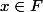
et donc
)
est liée et dans ce cas le resultat est evident )
et
)
une base orthonormé direct de
)
.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 29 invités
un espace euclidien,
, et
. On suppose
libre, et on note
.
de
,
.
, l'égalité :
(on effectuera des opérations élémentaires sur le déterminant d'ordre
).