Décimales de Pi et tableur
15 messages
- Page 1 sur 1
Décimales de Pi et tableur
Bonjour à tous,
J'aimerais introduire les probabilités en classe de seconde par le calcul des fréquences d'apparition des décimales de Pi.
Pour cela, il me faudrait rentrer un certain nombre de décimales dans un fichier tableur à raison d'une décimale par cellule... Quelqu'un a-t-il un tuyau ? Un lien vers un tel fichier dispo en ligne ?
Merci à tous !
J'aimerais introduire les probabilités en classe de seconde par le calcul des fréquences d'apparition des décimales de Pi.
Pour cela, il me faudrait rentrer un certain nombre de décimales dans un fichier tableur à raison d'une décimale par cellule... Quelqu'un a-t-il un tuyau ? Un lien vers un tel fichier dispo en ligne ?
Merci à tous !
Re: Décimales de Pi et tableur
Bonjour,
Tu peux trouver des fichiers texte sur le web avec un million de décimales de pi, par exemple 100 décimales par ligne.
Tu télécharges un tel fichier, tu l'ouvres dans un éditeur de texte, tu gardes le nombre de lignes que tu souhaites, par exemple 100 pour avoir 10000 décimales.
Ensuite tu utilises la fonction "rechercher et remplacer" de ton éditeur pour remplacer
0 par 0;
1 par 1;
2 par 2;
etc.
Tu as maintenant toutes les décimales séparées par des ;
Tu importes ensuite ce fichier texte dans ton tableur, en indiquant le ; comme séparateur.
Tu te retrouves, en poursuivant l'exemple, avec un tableau de 100 lignes et 100 colonnes contenant les 10 000 premières décimales de pi, une décimale par cellule.
PS. Tout le monde pense que les décimales de pi sont équiréparties. Personne n'est capable de le démontrer. Personne n'est même capable de démontrer qu'il y a une infinité de 5, par exemple, dans le développement décimal de pi.
PPS. J'ai suivi la procédure que j'ai indiquée ci-dessus, et grâce au tableau obtenu et à la commande NB.SI j'ai obtenu pour les 10 000 premières décimales :
Tu peux trouver des fichiers texte sur le web avec un million de décimales de pi, par exemple 100 décimales par ligne.
Tu télécharges un tel fichier, tu l'ouvres dans un éditeur de texte, tu gardes le nombre de lignes que tu souhaites, par exemple 100 pour avoir 10000 décimales.
Ensuite tu utilises la fonction "rechercher et remplacer" de ton éditeur pour remplacer
0 par 0;
1 par 1;
2 par 2;
etc.
Tu as maintenant toutes les décimales séparées par des ;
Tu importes ensuite ce fichier texte dans ton tableur, en indiquant le ; comme séparateur.
Tu te retrouves, en poursuivant l'exemple, avec un tableau de 100 lignes et 100 colonnes contenant les 10 000 premières décimales de pi, une décimale par cellule.
PS. Tout le monde pense que les décimales de pi sont équiréparties. Personne n'est capable de le démontrer. Personne n'est même capable de démontrer qu'il y a une infinité de 5, par exemple, dans le développement décimal de pi.
* un nombre est dit normal si ses" décimales" dans n'importe quelle base sont équiréparties.wikipedia a écrit:Il est extrêmement difficile de démontrer la normalité de nombres pourtant simples. Par exemple, on ne sait pas siou
sont normaux* (mais des expériences numériques font conjecturer qu'ils le sont). On ne sait même pas démontrer qu'un chiffre donné apparaît une infinité de fois dans le développement décimal de ces constantes.
PPS. J'ai suivi la procédure que j'ai indiquée ci-dessus, et grâce au tableau obtenu et à la commande NB.SI j'ai obtenu pour les 10 000 premières décimales :
- Code: Tout sélectionner
chiffre occurrences
0 968
1 1026
2 1021
3 974
4 1012
5 1046
6 1021
7 970
8 948
9 1014
total 10000
Re: Décimales de Pi et tableur
C'est même vrai pour tout nombre qui n'est pas dyadique. Tu devrais faire une publication sur ce résultat. 
Re: Décimales de Pi et tableur
On peut s'amuser avec les décimales de pi sur un tableur.
On peut encore mieux s'amuser avec Python.
J'ai récupéré sur mon bureau le fichier de nom "PI1000000.txt" qui donne un million de décimales de pi et qui se trouve ici. Je mets en place les choses :
Ensuite, j'ai étudié le succès de différentes stratégies pour jouer au jeu "deviner la prochaîne décimale de pi" (si vous devinez juste, vous gagnez 9, sinon vous perdez 1). J'imagine quatre joueurs avec des stratégies différentes : A joue le chiffre qui est le moins sorti, B joue le chiffre qui est le plus sorti, C joue toujours 0, D joue le chiffre précédent. Voici un code qui retourne les listes des gains des joueurs pour n*100 décimales :
Voila, on peut voir ce qui ce passe quand on va jusqu'au million :
Voici le graphique obtenu :

Cette petite expérience peut questionner un certain nombre d'idées reçues, du genre
"Il vaut mieux jouer le chiffre qui est en retard"
"C'est idiot de parier sur le chiffre qui vient de sortir"
...
En fait, si l'on suppose que les chiffres sont tirés de manière indépendante et équiprobable, les quatre stratégies se valent ; aucune n'est meilleure que l'autre.
On peut encore mieux s'amuser avec Python.
J'ai récupéré sur mon bureau le fichier de nom "PI1000000.txt" qui donne un million de décimales de pi et qui se trouve ici. Je mets en place les choses :
- Code: Tout sélectionner
with open('../Bureau/PI1000000.txt','r') as fichier :
text=fichier.read()
L=text.splitlines()
import matplotlib.pyplot as plt
Ensuite, j'ai étudié le succès de différentes stratégies pour jouer au jeu "deviner la prochaîne décimale de pi" (si vous devinez juste, vous gagnez 9, sinon vous perdez 1). J'imagine quatre joueurs avec des stratégies différentes : A joue le chiffre qui est le moins sorti, B joue le chiffre qui est le plus sorti, C joue toujours 0, D joue le chiffre précédent. Voici un code qui retourne les listes des gains des joueurs pour n*100 décimales :
- Code: Tout sélectionner
def Partie(n) :
GainsA=[0]; GainsB=[0]; GainsC=[0]; GainsD=[0]
Scores=10*[0]
precedent=3
retard=0
avance=9
for ligne in L[:n] :
for car in ligne :
chiffre=int(car)
if chiffre==retard : GainsA.append(GainsA[-1]+9)
else : GainsA.append(GainsA[-1]-1)
if chiffre==avance : GainsB.append(GainsB[-1]+9)
else : GainsB.append(GainsB[-1]-1)
if chiffre==0 : GainsC.append(GainsC[-1]+9)
else : GainsC.append(GainsC[-1]-1)
if chiffre==precedent : GainsD.append(GainsD[-1]+9)
else : GainsD.append(GainsD[-1]-1)
Scores[chiffre]+=1
precedent=chiffre
retard=Scores.index(min(Scores))
avance=Scores.index(max(Scores))
return GainsA, GainsB, GainsC, GainsD
Voila, on peut voir ce qui ce passe quand on va jusqu'au million :
- Code: Tout sélectionner
GA,GB,GC,GD=Partie(10000)
fig, ax = plt.subplots()
ax.plot(GA, label='Gains A')
ax.plot(GB, label='Gains B')
ax.plot(GC, label='Gains C')
ax.plot(GD, label='Gains D')
ax.set_title("Historique des gains")
ax.legend()
Voici le graphique obtenu :

Cette petite expérience peut questionner un certain nombre d'idées reçues, du genre
"Il vaut mieux jouer le chiffre qui est en retard"
"C'est idiot de parier sur le chiffre qui vient de sortir"
...
En fait, si l'on suppose que les chiffres sont tirés de manière indépendante et équiprobable, les quatre stratégies se valent ; aucune n'est meilleure que l'autre.
Re: Décimales de Pi et tableur
L'intérêt des courbes représentées plus haut, c'est qu'on voit qu'il n'y a aucun classement stable entre les stratégies A, B, C, D. Il serait complètement idiot d'arrêter à un nombre fixe de décimales (par exemple 10 000) et de tirer des conclusions sur le classement à cette étape. Voici par exemple les classements par étape de 100 000 décimales entre 100 000 et 1 000 000 :
['A', 'B', 'C', 'D']
['C', 'B', 'A', 'D']
['B', 'C', 'A', 'D']
['B', 'C', 'A', 'D']
['D', 'B', 'A', 'C']
['B', 'C', 'D', 'A']
['B', 'D', 'C', 'A']
['B', 'D', 'A', 'C']
['D', 'B', 'C', 'A']
['D', 'B', 'C', 'A']
On voit que ça n'arrête pas de changer, ce qui est tout à fait logique.
['A', 'B', 'C', 'D']
['C', 'B', 'A', 'D']
['B', 'C', 'A', 'D']
['B', 'C', 'A', 'D']
['D', 'B', 'A', 'C']
['B', 'C', 'D', 'A']
['B', 'D', 'C', 'A']
['B', 'D', 'A', 'C']
['D', 'B', 'C', 'A']
['D', 'B', 'C', 'A']
On voit que ça n'arrête pas de changer, ce qui est tout à fait logique.
Re: Décimales de Pi et tableur
On peut modifier le graphique ci-dessus pour lui faire enregistrer
non pas l'historique des gains, mais l'historique des fréquences de succès. Voici la modification du code (on ne fait afficher l'historique qu'à partir de la 100 000e décimale).

On constate sans surprise que les fréquences de succès des quatre stratégies tendent toutes vers 1/10. Mais on constate aussi bien sûr que les positions relatives des quatre courbes coïncident entre les deux graphiques ; elles s'entremêlent tout autant.
non pas l'historique des gains, mais l'historique des fréquences de succès. Voici la modification du code (on ne fait afficher l'historique qu'à partir de la 100 000e décimale).
- Code: Tout sélectionner
def Succes(G) :
return [(G[k]+k)/10/k for k in range(1,len(G))]
SA=Succes(GA); SB=Succes(GB); SC=Succes(GC); SD=Succes(GD)
fig, ax = plt.subplots()
ax.plot(range(10**5,10**6),SA[10**5:], label='Succès A')
ax.plot(range(10**5,10**6),SB[10**5:], label='Succès B')
ax.plot(range(10**5,10**6),SC[10**5:], label='Succès C')
ax.plot(range(10**5,10**6),SD[10**5:], label='Succès D')
ax.set_title("Historique des fréquences de succès")
ax.legend()

On constate sans surprise que les fréquences de succès des quatre stratégies tendent toutes vers 1/10. Mais on constate aussi bien sûr que les positions relatives des quatre courbes coïncident entre les deux graphiques ; elles s'entremêlent tout autant.
Re: Décimales de Pi et tableur
Si on joue au même jeu avec  par exemple, est-ce que ça donne le même résultat (ou la même absence de résultat, selon le point de vue).
par exemple, est-ce que ça donne le même résultat (ou la même absence de résultat, selon le point de vue).
Re: Décimales de Pi et tableur
Qu'est-ce qui te fait penser que ça pourrait être différent avec 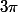 ?
?
Je suis presque sûr (au sens où la probabilité que je me trompe est 0%, mais que ce n'est pas impossible) que l'on aboutira aux mêmes conclusions :
1°) Aucune des stratégies n'est préférable à une autre.
2°) Pour toutes ces stratégies, la fréquence des succès tend vers 1/10.
Je suis presque sûr (au sens où la probabilité que je me trompe est 0%, mais que ce n'est pas impossible) que l'on aboutira aux mêmes conclusions :
1°) Aucune des stratégies n'est préférable à une autre.
2°) Pour toutes ces stratégies, la fréquence des succès tend vers 1/10.
Modifié en dernier par GaBuZoMeu le 26 Mar 2020, 18:26, modifié 1 fois.
Re: Décimales de Pi et tableur
Ce qui me fait penser que bla bla ...
Strictement rien.
Mais si par le plus grand des hasards, c'était différent, ce serait amusant. Et puis c'est comme un petit challenge
Et l'intérêt, ce serait de voir si les intervalles où la stratégie A est gagnante avec PI sont les mêmes que les intervalles où la stratégie A est gagnante avec 3 PI. Et respectivement, pour les stratégies B C et D.
A priori, oui, mais je n'en sais rien.
Intérêt tout relatif , j'avoue.
Je me suis posé une autre question aussi. Plus théorique.
Avec les 10000 premières décimales, on a vu qu'on a 968 fois 0, 1026 fois 1 , etc etc 948 fois 8 et 1014 fois 9.
On a de petits écarts autour de 1000 pour chacun des 10 compteurs.
Je dis "petits écarts", mais ces écarts sont ils réellement petits ?
Autrement dit, si on lance 10000 fois un dé à 10 faces, le fait d'obtenir seulement 948 fois le chiffre 8, c'est dans la norme, ou c'est atypique ?
PS : je suis allé voir la page Wikipedia sur les nombres normaux, et il y est dit : Le produit d'un nombre normal en base b par un rationnel non nul est normal en base b
Comme on est à peu près convaincu que Pi est normal, ça répond quasiment à ma première question.
Strictement rien.
Mais si par le plus grand des hasards, c'était différent, ce serait amusant. Et puis c'est comme un petit challenge
Et l'intérêt, ce serait de voir si les intervalles où la stratégie A est gagnante avec PI sont les mêmes que les intervalles où la stratégie A est gagnante avec 3 PI. Et respectivement, pour les stratégies B C et D.
A priori, oui, mais je n'en sais rien.
Intérêt tout relatif , j'avoue.
Je me suis posé une autre question aussi. Plus théorique.
Avec les 10000 premières décimales, on a vu qu'on a 968 fois 0, 1026 fois 1 , etc etc 948 fois 8 et 1014 fois 9.
On a de petits écarts autour de 1000 pour chacun des 10 compteurs.
Je dis "petits écarts", mais ces écarts sont ils réellement petits ?
Autrement dit, si on lance 10000 fois un dé à 10 faces, le fait d'obtenir seulement 948 fois le chiffre 8, c'est dans la norme, ou c'est atypique ?
PS : je suis allé voir la page Wikipedia sur les nombres normaux, et il y est dit : Le produit d'un nombre normal en base b par un rationnel non nul est normal en base b
Comme on est à peu près convaincu que Pi est normal, ça répond quasiment à ma première question.
Re: Décimales de Pi et tableur
L'écart-type pour la loi binomiale qui compte le nombre de succès sur  épreuves de Bernoulli indépendantes de probabilité de succès
épreuves de Bernoulli indépendantes de probabilité de succès  est
est }= \dfrac3{10}\sqrt{n}) , ce qui fait 30 pour
, ce qui fait 30 pour  .
.
Sur l'échantillon fourni par les 10 décimales, avec une espérance de 1000 occurrences sur 10 000, l'écart-type calculé est 30,5.
Pi fait vraiment tout ce qu'il faut pour faire croire qu'il est normal.
Sur l'échantillon fourni par les 10 décimales, avec une espérance de 1000 occurrences sur 10 000, l'écart-type calculé est 30,5.
Pi fait vraiment tout ce qu'il faut pour faire croire qu'il est normal.
Re: Décimales de Pi et tableur
En parlant de "normal" :
On peut explorer, toujours avec python, les occurrences de suites de 3 chiffres dans le premier million de décimales de pi :

suite qui apparaît le moins : 067 avec 898 occurrences
suite qui apparaît le plus : 654 avec 1092 occurrences
PS. L'analyse théorique de cette situation présente quelques difficultés.
L'idée générale est que la suite des décimales de présente toutes les caractéristiques d'une suite
présente toutes les caractéristiques d'une suite ) de chiffres tirés au hasard de manière indépendante et équiprobable.
de chiffres tirés au hasard de manière indépendante et équiprobable.
On se donne ici une chaîne de trois chiffres et on compte le nombre d'occurrences de
et on compte le nombre d'occurrences de  dans la chaîne des
dans la chaîne des  premiers chiffres. C'est la somme des variables de Bernoulli
premiers chiffres. C'est la somme des variables de Bernoulli 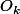 qui valent 1 si
qui valent 1 si  et 0 sinon, pour
et 0 sinon, pour  allant de 0 à
allant de 0 à  . Ces variables de Bernoulli ont toutes pour espérance
. Ces variables de Bernoulli ont toutes pour espérance 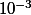 . Problème : elles ne sont pas indépendantes. Le nombre d'occurrences ne suit donc pas une loi binomiale, et la loi suivie par le nombre d'occurrences dépend de la forme de la chaîne
. Problème : elles ne sont pas indépendantes. Le nombre d'occurrences ne suit donc pas une loi binomiale, et la loi suivie par le nombre d'occurrences dépend de la forme de la chaîne  : il faut distinguer les cas
: il faut distinguer les cas  ,
,  et les autres cas. Je reviendrai plus en détail sur ce point.
et les autres cas. Je reviendrai plus en détail sur ce point.
On peut explorer, toujours avec python, les occurrences de suites de 3 chiffres dans le premier million de décimales de pi :
- Code: Tout sélectionner
with open('../Bureau/PI1000000.txt','r') as fichier :
text=fichier.read().replace("\n","")
import matplotlib.pyplot as plt
def Occurrences(n,chaine) :
L = 10**n*[0]
for i in range(len(chaine)-n+1) :
L[int(chaine[i:i+n])]+=1
return L
L3=Occurrences(3,text)
_ = plt.hist(L3, bins='auto')
plt.title("Histogramme des nombres d'occurrences\n\
des 1000 suites de 3 chiffres\n\
dans le premier million de décimales de pi")
plt.show()

- Code: Tout sélectionner
mini=min(L3)
suitemini=str(L3.index(mini)).zfill(3)
print("suite qui apparaît le moins :",suitemini,\
"avec",mini,"occurrences")
maxi=max(L3)
suitemaxi=str(L3.index(maxi)).zfill(3)
print("suite qui apparaît le plus :",suitemaxi,\
"avec",maxi,"occurrences")
suite qui apparaît le moins : 067 avec 898 occurrences
suite qui apparaît le plus : 654 avec 1092 occurrences
PS. L'analyse théorique de cette situation présente quelques difficultés.
L'idée générale est que la suite des décimales de
On se donne ici une chaîne de trois chiffres
Re: Décimales de Pi et tableur
Avant de revenir au sujet ci-dessus, on s'intéresse à un problème plus simple. On découpe la suite des décimales de pi par tranches de 3, et on compte, pour chaque chaîne de trois chiffres, le nombre d'occurrences dans cette suite de tranches. Ça revient bien sûr à s'intéresser à l'apparition des "décimales" de pi en base 1000. Notre million de décimales nous permet d'avoir 333 333 tranches de 3.
Comme on est persuadé (sans en avoir la démonstration) que pi est normal en base 1000, on s'attend à ce que la moyenne du nombre d'apparition des chaînes de trois chiffres dans la suite des tranches soit 333 333 x 1/1000 = 333,333. On s'attend aussi à ce que la variance soit 333 333 x 1/1000 x (1 - 1/1000) = 333 (à un chouïa près). C'est ce qu'on aurait avec une loi binomiale de paramètres n = 333 333 et p = 1/1000.
Voyons si ces prévisions sont correctes. J'utilise toujours la chaîne "text" qui est la chaîne du million de décimales de pi.

Voyons maintenant la moyenne et la variance :
la variance est 332.7
Waouh !
PS. Si vous vous ennuyez en ces temps de confinement, vous pouvez toujours jeter un oeil sur ce fil. Ça vaut son pesant de moutarde. Pour compléter le tableau, on pourra lire ici la "démonstration" du fait que pi est normal.
Comme on est persuadé (sans en avoir la démonstration) que pi est normal en base 1000, on s'attend à ce que la moyenne du nombre d'apparition des chaînes de trois chiffres dans la suite des tranches soit 333 333 x 1/1000 = 333,333. On s'attend aussi à ce que la variance soit 333 333 x 1/1000 x (1 - 1/1000) = 333 (à un chouïa près). C'est ce qu'on aurait avec une loi binomiale de paramètres n = 333 333 et p = 1/1000.
Voyons si ces prévisions sont correctes. J'utilise toujours la chaîne "text" qui est la chaîne du million de décimales de pi.
- Code: Tout sélectionner
def Basen(n,chaine) :
L = 10**n*[0]
for i in range(len(chaine)//3) :
L[int(chaine[3*i:3*i+n])]+=1
return L
Lbase3=Basen(3,text)
_ = plt.hist(Lbase3, bins='auto')
plt.title("Histogramme des nombres d'occurrences\n\
des 1000 suites de 3 chiffres dans la liste\n\
des 333333 premières tranches de 3 décimales")
plt.show()

Voyons maintenant la moyenne et la variance :
- Code: Tout sélectionner
moyenne=sum(occ for occ in Lbase3)/len(Lbase3)
print("la moyenne est {:0,.1f}".format(moyenne))
variance=sum((occ-333.333)**2 for occ in Lbase3)/len(Lbase3)
print("la variance est {:0,.1f}".format(variance))
la variance est 332.7
Waouh !
PS. Si vous vous ennuyez en ces temps de confinement, vous pouvez toujours jeter un oeil sur ce fil. Ça vaut son pesant de moutarde. Pour compléter le tableau, on pourra lire ici la "démonstration" du fait que pi est normal.

Re: Décimales de Pi et tableur
Reprenons maintenant le problème que nous avons laissé.
On a une suite) de chiffres tirés au hasard de manière indépendante et équiprobable, de longueur
de chiffres tirés au hasard de manière indépendante et équiprobable, de longueur 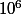 .
.
On se donne une chaîne de trois chiffres ; pour
; pour  allant de 0 à N=999 997, on définit la variable de Bernoulli
allant de 0 à N=999 997, on définit la variable de Bernoulli 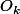 qui vaut 1 si
qui vaut 1 si  et 0 sinon. Le nombre d'occurrences de
et 0 sinon. Le nombre d'occurrences de  dans la chaîne des
dans la chaîne des  est
est  . Les variables de Bernoulli
. Les variables de Bernoulli 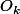 ont toutes pour espérance
ont toutes pour espérance 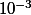 et donc l'espérance du nombre d'occurences de
et donc l'espérance du nombre d'occurences de  est
est  , soit 1000 à un chouïa près. Problème : les
, soit 1000 à un chouïa près. Problème : les 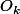 ne sont pas indépendantes (car ici on considère des occurrences en des emplacements qui peuvent se chevaucher), donc le nombre d'occurrences ne suit pas une loi binomiale,
ne sont pas indépendantes (car ici on considère des occurrences en des emplacements qui peuvent se chevaucher), donc le nombre d'occurrences ne suit pas une loi binomiale,
Il y a trois cas à distinguer suivant la forme de .
.
Si c'est un triplet, c-à-d. si , on a :
, on a :
 = 10^{-4}) ,
,  = 10^{-5}) et
et  = 10^{-6}) si
si  .
.
En effet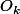 et
et  valent 1 quand on rencontre "aaaa" à partir de l'indice
valent 1 quand on rencontre "aaaa" à partir de l'indice  et
et 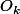 et
et  valent 1 quand on rencontre "aaaaa" à partir de l'indice
valent 1 quand on rencontre "aaaaa" à partir de l'indice  .
.
Si , on a :
, on a :
 = 0) ,
,  = 10^{-5}) et
et  = 10^{-6}) si
si  .
.
En effet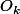 et
et  ne peuvent pas valoir 1 en même temps et
ne peuvent pas valoir 1 en même temps et 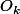 et
et  valent 1 quand on rencontre "ababa" à partir de l'indice
valent 1 quand on rencontre "ababa" à partir de l'indice 
Dans les autres cas on a :
 = 0) ,
,  = 0}) et
et  = 10^{-6}) si
si  .
.
En effet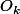 et
et  ne peuvent pas valoir 1 en même temps, pas plus que
ne peuvent pas valoir 1 en même temps, pas plus que 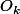 et
et  .
.
Si les variables de Bernoulli étaient indépendantes, la variance de leur somme serait
variables de Bernoulli étaient indépendantes, la variance de leur somme serait ) , ce qui fait 1000 à un chouïa près. On peut partir de ça pour donner la variance du nombre d'occurrences de
, ce qui fait 1000 à un chouïa près. On peut partir de ça pour donner la variance du nombre d'occurrences de  en fonction de la forme de
en fonction de la forme de  , en utilisant ce qui vient d'être dit.
, en utilisant ce qui vient d'être dit.
Pour , la variance est
, la variance est (10^{-4}-10^{-6}) +2(N-2)(10^{-5}-10^{-6})) , soit 1216 à un chouïa près.
, soit 1216 à un chouïa près.
Pour , la variance est
, la variance est (0-10^{-6}) +2(N-2)(10^{-5}-10^{-6})) , soit 1016 à un chouïa près.
, soit 1016 à un chouïa près.
Pour [les autres , la variance est
, la variance est (0-10^{-6}) +2(N-2)(0-10^{-6})) , soit 996 à un chouïa près.
, soit 996 à un chouïa près.
Maintenant, comparons ça avec ce qui se passe pour les décimales de . La liste L[3] des nombres d'occurrences est celle construite avec le code de ce message.
. La liste L[3] des nombres d'occurrences est celle construite avec le code de ce message.
Pour les triplets :
la variance est 1253.0
Pour une moyenne attendue de 1000 et une variance attendue de 1216. Pas mal (on n'a que 10 triplets)
Pour les aba :
la variance est 868.0
pour une moyenne attendue de 1000 et une variance attendue de 1016. Hola, la variance ne va pas trop fort !
Pour les autres :
la variance est 963.9
pour une moyenne attendue de 1000 et une variance attendue de 996.
Me suis-je trompé pour les aba ? Est-ce que la différence importante entre la variance attendue et la variance constatée reste dans les clous ? On n'a que 90 aba. Si vous avez un avis ...
On a une suite
On se donne une chaîne de trois chiffres
Il y a trois cas à distinguer suivant la forme de
Si c'est un triplet, c-à-d. si
En effet
Si
En effet
Dans les autres cas on a :
En effet
Si les
Pour
Pour
Pour [les autres
Maintenant, comparons ça avec ce qui se passe pour les décimales de
Pour les triplets :
- Code: Tout sélectionner
triples=[k*111 for k in range(10)]
Ltriples=[L3[n] for n in triples]
moyenne=sum(occ for occ in Ltriples)/len(triples)
variance =sum((occ-1000)**2 for occ in Ltriples)/len(triples)
print("la moyenne est {:0.1f}".format(moyenne))
print("la variance est {:0.1f}".format(variance))
la variance est 1253.0
Pour une moyenne attendue de 1000 et une variance attendue de 1216. Pas mal (on n'a que 10 triplets)
Pour les aba :
- Code: Tout sélectionner
aba=[k*101+l*10 for l in range(10) for k in range(l)]\
+[k*101+l*10 for l in range(10) for k in range(l+1,10)]
Laba=[L3[n] for n in aba]
moyenne=sum(occ for occ in Laba)/len(aba)
variance =sum((occ-1000)**2 for occ in Laba)/len(aba)
print("la moyenne est {:0.1f}".format(moyenne))
print("la variance est {:0.1f}".format(variance))
la variance est 868.0
pour une moyenne attendue de 1000 et une variance attendue de 1016. Hola, la variance ne va pas trop fort !
Pour les autres :
- Code: Tout sélectionner
autre = lambda n : n not in triples and n not in aba
autres=[n for n in range(10**3) if autre(n)]
Lautres=[L3[n] for n in autres]
moyenne=sum(occ for occ in Lautres)/len(autres)
variance =sum((occ-1000)**2 for occ in Lautres)/len(autres)
print("la moyenne est {:0.1f}".format(moyenne))
print("la variance est {:0.1f}".format(variance))
la variance est 963.9
pour une moyenne attendue de 1000 et une variance attendue de 996.
Me suis-je trompé pour les aba ? Est-ce que la différence importante entre la variance attendue et la variance constatée reste dans les clous ? On n'a que 90 aba. Si vous avez un avis ...
Re: Décimales de Pi et tableur
En y réfléchissant, je pense que les calculs sont bons mais qu'il y a à la base une erreur de méthode : je fais le calcul de variance en fixant la chaîne de trois chiffres de forme aba et en prenant comme aléatoire la suite de chiffres dans laquelle je compte les occurrences de cette chaîne. Et d'un autre côté je fixe la suite de chiffres (celle des décimales de pi, certes très longue et dont on pense qu'elle a les caractéristiques d'une suite aléatoire avec tirages équiprobables et indépendants), et je fais varier les chaînes de 3 parmi toutes celles de la forme aba. Or il est intuitivement clair que les occurrences de aba ne sont pas "indépendantes" de celles de bab, par exemple (baba ou abab). Je ne sais pas si j'arriverai à préciser ça.
15 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 39 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
