Début série de Taylor
33 messages
- Page 1 sur 2 - 1, 2
Re: Début série de Taylor
Bonjour lazare,
les deux réponses que tu donnes sont justes,
par convention 0! = 1 et x^0 = 1 d'étend exceptionnellement ici en 0^0 = 1.
Cordialement,
les deux réponses que tu donnes sont justes,
par convention 0! = 1 et x^0 = 1 d'étend exceptionnellement ici en 0^0 = 1.
Cordialement,
Re: Début série de Taylor
lazare a écrit:le deux réponses donnent peut etre le même résultat ais il est important pour moi de savoir si la première est la simplification de la seconde ou pas.
Je ne le pense pas
La première (à mon avis mais mon avis voir l'inspecteur Callahan dans le lien làhttps://www.youtube.com/watch?v=iN_71I7fldA)
est une convention qui sert pour les fonctions en théorie des ensembles et la seconde c'est autre chose encore
Re: Début série de Taylor
Bonjour Lazare
Avez vous construit un tableau de dérivation?(attention rien à voir avec un tableau de comportement d'une fonction)
C'est prendre à la lettre une dérivation de fonction
on place des colonnes
première colonne x
deuxième colonne f(x)
troisième colonne df
quatrième colonne f'(x)
etc... et vous verrez que vous découvrirez des formules que wiki nous donne
Car il est important de savoir pourquoi un truc c'est comme ça et ça fait comme ça
et je sais que vous aimez les maths et n'êtes pas marié avec les formules du wiki
wiki est fait pour consolider un savoir mais pas pour le construire
Avez vous construit un tableau de dérivation?(attention rien à voir avec un tableau de comportement d'une fonction)
C'est prendre à la lettre une dérivation de fonction
on place des colonnes
première colonne x
deuxième colonne f(x)
troisième colonne df
quatrième colonne f'(x)
etc... et vous verrez que vous découvrirez des formules que wiki nous donne
Car il est important de savoir pourquoi un truc c'est comme ça et ça fait comme ça
et je sais que vous aimez les maths et n'êtes pas marié avec les formules du wiki
wiki est fait pour consolider un savoir mais pas pour le construire
Re: Début série de Taylor
Moi je vous aime bien Lazare
Vous savez moi j'ai découvert l'algèbre en faisant les poubelles (je cherchais des mégots de cigarettes pour faire mon paquet de tabac recyclé)
J'étais tombé sur un livre d'algèbre de Jacqueline Lelong-Ferrand (décédée en 2014)
et j'ai vite compris que si je voulais comprendre ce qu'elle dit il faudrait que je travaille un peu tout seul
Bref tout ça pour dire qu'en fait wiki c'est joli oui ok avec toutes les formules qu'il nous donne mais si on cherche à déduire des trucs sur les formules données sans savoir comment ces formules sont venus on va vite avoir des smilblicks en séries (à la place de celles qu'on voulait)
Vous savez moi j'ai découvert l'algèbre en faisant les poubelles (je cherchais des mégots de cigarettes pour faire mon paquet de tabac recyclé)
J'étais tombé sur un livre d'algèbre de Jacqueline Lelong-Ferrand (décédée en 2014)
et j'ai vite compris que si je voulais comprendre ce qu'elle dit il faudrait que je travaille un peu tout seul
Bref tout ça pour dire qu'en fait wiki c'est joli oui ok avec toutes les formules qu'il nous donne mais si on cherche à déduire des trucs sur les formules données sans savoir comment ces formules sont venus on va vite avoir des smilblicks en séries (à la place de celles qu'on voulait)
Re: Début série de Taylor
Bonsoir,
}=f) et
et }=(f^{(n)})')
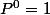 et
et 
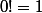 et
et != (n+1)\times n!)
Qu'est-ce que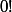 peut être d'autre que 1 ? Le nombre de permutations de l'ensemble vide est bien 1, n'est-ce pas ?
peut être d'autre que 1 ? Le nombre de permutations de l'ensemble vide est bien 1, n'est-ce pas ?
Qu'est-ce que
Re: Début série de Taylor
lazare a écrit: Haha et bien je suis pourtant bien le genre de personne naive prete a tout prendre à la lettre sur wikipedia.
mais je n'ai pas dit que wiki se trompe
je dit juste que wiki est là pour consolider un travail personnel à faire et qui permet d'éviter d'interpréter des résultats sans savoir comment ces résultats sont venus
Si vous effectuez votre tableau de dérivation (comme indiqué plus haut)
voilà ce que vous trouverez sous condition de dérivation successive mais cette condition vous vous la donnez vous même puisque c'est vous qui faites le tableau
prenez votre temps pour la retrouver en faisant votre tableau (papier+ stylo)
ici
en fait la dernière expression exprime l'intégrale avec la fonction et non avec la n-ième dérivée successive
c'est l'exploitation complète du tableau dont le but est d'exprimer l'intégrale uniquement avec la fonction
Re: Début série de Taylor
NB: si vous faites votre tableau vous ferez l'intégrale en "acte"
un passage à la ligne correspond à une différentielle dx
un passage à la ligne correspond à une différentielle dx
Re: Début série de Taylor
Bon après on doit se dire de la dernière expression que c'est valable si elle est au moins de classe 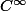
Comme on a construit le tableau sous cette condition on peut se permettre de le dire mais pas de s'avancer plus loin
Si on prend la formule telle qu'elle mais qu'on ne sait pas comment elle est faite on peut en déduire des choses complètement fausses
d'où à mon avis l'intérêt et bon le tableau prend un peu de temps à faire (c'est pas tellement sur le nombre de colonnes mais c'est un peu 'chiant' vu qu'on somme dx et qu'il faut ensuite trouver une formule générale à la ligne k.dx
Après on doit faire attention car le passage d'une ligne à l'autre se fait de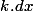 à
à .dx)
Quand on a une fonction il faut bien veiller à regarder que son domaine de définition coïncide avec celle de notre tableau
voilà ... bon courage
ça va vous prendre un peu de temps mais bon mon avis est que ce ne sera pas du temps perdu mais mon avis évidemment est contrebalancé avec l'opinion des avis donné par l'inspecteur Callahan
Inspecteur Harry numéro je ne sais plus lequel (je crois que c'est dans sudden impact mais bon là je ne sais plus exactement on va dire environ vers là-bas)
Comme on a construit le tableau sous cette condition on peut se permettre de le dire mais pas de s'avancer plus loin
Si on prend la formule telle qu'elle mais qu'on ne sait pas comment elle est faite on peut en déduire des choses complètement fausses
d'où à mon avis l'intérêt et bon le tableau prend un peu de temps à faire (c'est pas tellement sur le nombre de colonnes mais c'est un peu 'chiant' vu qu'on somme dx et qu'il faut ensuite trouver une formule générale à la ligne k.dx
Après on doit faire attention car le passage d'une ligne à l'autre se fait de
Quand on a une fonction il faut bien veiller à regarder que son domaine de définition coïncide avec celle de notre tableau
voilà ... bon courage
ça va vous prendre un peu de temps mais bon mon avis est que ce ne sera pas du temps perdu mais mon avis évidemment est contrebalancé avec l'opinion des avis donné par l'inspecteur Callahan
Inspecteur Harry numéro je ne sais plus lequel (je crois que c'est dans sudden impact mais bon là je ne sais plus exactement on va dire environ vers là-bas)
Re: Début série de Taylor
Bonsoir GaBuZoMeu
je te réponds sur le nombre de permutations de l'ensemble vide .
Une permutation de l'ensemble vide ne veut rien dire à priori , donc , à priori , il n'y en a pas ; sauf si l'on sait définir une fonction de A dans B comme une partie du produit cartésien AxB .
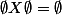 (faut il encore expliquer pourquoi) , ce produit ne possede qu'une partie . Faut il encore expliquer la bijectivité de cette partie .
(faut il encore expliquer pourquoi) , ce produit ne possede qu'une partie . Faut il encore expliquer la bijectivité de cette partie .
je te réponds sur le nombre de permutations de l'ensemble vide .
Une permutation de l'ensemble vide ne veut rien dire à priori , donc , à priori , il n'y en a pas ; sauf si l'on sait définir une fonction de A dans B comme une partie du produit cartésien AxB .
Re: Début série de Taylor
Bonjour Tournesol,
Tu as vraiment si peur que ça du vide ?
"Une permutation de l'ensemble vide ne veut rien dire à priori" : ça c'est un a priori qui ne repose sur rien. Une permutation de l'ensemble vide, ça a exactement la même définition qu'une permutation d'un ensemble quelconque : une bijection de l'ensemble sur lui-même.
"sauf si l'on sait définir une fonction de A dans B comme une partie du produit cartésien AxB"
Ce n'est pas ça la définition d'une application de n'importe quel ensemble A dans n'importe quel ensemble B ? Ensemblstement, tu définis une fonction autrement que par son graphe ?
Il y a une et une seule application de l'ensemble vide dans n'importe quel ensemble E. Son graphe est l'ensemble vide.
L'unique application de l'ensemble vide dans l'ensemble vide est bijective. Tu en doutes ? Tu sais pourtant bien que toute formule du genre) est vraie.
est vraie.
Pourquoi cet ostracisme envers l'ensemble vide ? L'ensemble vide est un ensemble comme un autre, laissons-le vivre sa vie et contentons-nous de lui appliquer la règle commune valable pour tous les ensembles.
Petits exercices :
- Donner une base de l'espace vectoriel nul.
- Quel est le déterminant de l'unique endomorphisme de l'espace vectoriel nul ?
Tu as vraiment si peur que ça du vide ?
"Une permutation de l'ensemble vide ne veut rien dire à priori" : ça c'est un a priori qui ne repose sur rien. Une permutation de l'ensemble vide, ça a exactement la même définition qu'une permutation d'un ensemble quelconque : une bijection de l'ensemble sur lui-même.
"sauf si l'on sait définir une fonction de A dans B comme une partie du produit cartésien AxB"
Ce n'est pas ça la définition d'une application de n'importe quel ensemble A dans n'importe quel ensemble B ? Ensemblstement, tu définis une fonction autrement que par son graphe ?
Il y a une et une seule application de l'ensemble vide dans n'importe quel ensemble E. Son graphe est l'ensemble vide.
L'unique application de l'ensemble vide dans l'ensemble vide est bijective. Tu en doutes ? Tu sais pourtant bien que toute formule du genre
Pourquoi cet ostracisme envers l'ensemble vide ? L'ensemble vide est un ensemble comme un autre, laissons-le vivre sa vie et contentons-nous de lui appliquer la règle commune valable pour tous les ensembles.
Petits exercices :
- Donner une base de l'espace vectoriel nul.
- Quel est le déterminant de l'unique endomorphisme de l'espace vectoriel nul ?
Re: Début série de Taylor
Bonjour GaBuZoMeu et merci pour les exos .
Je t'enverrais mes solutions mais après avoir révisés les liens entre et la logique .
et la logique .
Bien que je ne maitrise pas l'usage de , je connais les définitions ensemblistes d'une correspondance et de ses différents types .
, je connais les définitions ensemblistes d'une correspondance et de ses différents types .
Une caractérisation des bijections qui me sera peut être utile :la correspondance (A,B,G) est une bijection ssi (A,B,G) et (B,A,) sont des applications .
sont des applications .
Je t'enverrais mes solutions mais après avoir révisés les liens entre
Bien que je ne maitrise pas l'usage de
Une caractérisation des bijections qui me sera peut être utile :la correspondance (A,B,G) est une bijection ssi (A,B,G) et (B,A,
Re: Début série de Taylor
Bonjour,
C'est un joli plaidoyer pour l'ensemble vide que tu fais là GaBuZoMeu mais j'ai quand même l'impression, moi aussi, qu'il n'est pas comme les autres. Si tu dis qu'on peut appliquer les définitions communes, j'en deduis la réponse à tes exercices (je laisse tournesol y réfléchir) m'enfin quand même, je n'arrive pas à leur donner le même "sens" qu'en temps normal. Ceci dit, je t'accorde que c'est juste ma perception et qu'elle ne repose sur aucun argument sérieux, je présume qu'une fois habituée, elle disparait.
C'est un joli plaidoyer pour l'ensemble vide que tu fais là GaBuZoMeu mais j'ai quand même l'impression, moi aussi, qu'il n'est pas comme les autres. Si tu dis qu'on peut appliquer les définitions communes, j'en deduis la réponse à tes exercices (je laisse tournesol y réfléchir) m'enfin quand même, je n'arrive pas à leur donner le même "sens" qu'en temps normal. Ceci dit, je t'accorde que c'est juste ma perception et qu'elle ne repose sur aucun argument sérieux, je présume qu'une fois habituée, elle disparait.
Re: Début série de Taylor
tournesol a écrit:Une caractérisation des bijections qui me sera peut être utile :la correspondance (A,B,G) est une bijection ssi (A,B,G) et (B,A,sont des applications .

Re: Début série de Taylor
Bonjour
Il est important aussi de voir que l'ensemble vide se travaille (et c'est là que je suis d'accord avec GaBuZoMeu)
(Mais juste que pour les séries de Taylor on peut les aborder comme je l'ai dit plus haut sans entrer dans ce travail là sur l'ensemble vide et de partir de la convention admise 0!=1)
Je propose deux petits exos :
1.La partition de l'ensemble vide est lui-même
2. Montrer que
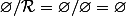
ici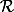 est une relation d'équivalence
est une relation d'équivalence
Il est important aussi de voir que l'ensemble vide se travaille (et c'est là que je suis d'accord avec GaBuZoMeu)
(Mais juste que pour les séries de Taylor on peut les aborder comme je l'ai dit plus haut sans entrer dans ce travail là sur l'ensemble vide et de partir de la convention admise 0!=1)
Je propose deux petits exos :
1.La partition de l'ensemble vide est lui-même
2. Montrer que
ici
Modifié en dernier par azf le 14 Sep 2021, 15:32, modifié 1 fois.
Re: Début série de Taylor
Pour ton premier exo:
base en tant que partie génératrice minimale (base non ordonnée) :
base en tant que famille génératrice minimale:()
Bien que non nécessaire ,il me parait interressant de montrer qu'elle est libre (maximale étant évident car {0} est liée). je dois réviser pour cela , en particulier les sommes indexées sur
base en tant que partie génératrice minimale (base non ordonnée) :
base en tant que famille génératrice minimale:(
Bien que non nécessaire ,il me parait interressant de montrer qu'elle est libre (maximale étant évident car {0} est liée). je dois réviser pour cela , en particulier les sommes indexées sur
Re: Début série de Taylor
Pour le premier j'ai ça
La définition de la partition d'un ensemble est conditionnée par le fait que ses éléments qui constituent le recouvrement strict de cet ensemble ne soient pas vides
Tout ensemble recouvre l'ensemble vide et il le recouvre strictement si cet ensemble est l'ensemble vide
La partition de l'ensemble vide est donc vide et donc lui-même
La définition de la partition d'un ensemble est conditionnée par le fait que ses éléments qui constituent le recouvrement strict de cet ensemble ne soient pas vides
Tout ensemble recouvre l'ensemble vide et il le recouvre strictement si cet ensemble est l'ensemble vide
La partition de l'ensemble vide est donc vide et donc lui-même
Re: Début série de Taylor
Bien d'accord, la (il n'y en a qu'une) base de l'espace vectoriel nul est la famille vide.
Re: Début série de Taylor
Bonjour
pour la liberté dans le premier exo , le produit de rien ne resulte pas des définitions mais est égal au neutre par convention lorsqu'il existe . Donc pour moi , on ne peut pas déterminer si la famille vide est libre ou liée .
Pour le deuxieme exo , je cale : qu'est ce qu'une forme 0 linéaire alternée ?
pour la liberté dans le premier exo , le produit de rien ne resulte pas des définitions mais est égal au neutre par convention lorsqu'il existe . Donc pour moi , on ne peut pas déterminer si la famille vide est libre ou liée .
Pour le deuxieme exo , je cale : qu'est ce qu'une forme 0 linéaire alternée ?
33 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
