Je n'ai moi même jamais reçu l'aspect juridique de la culture du vide , c'est à dire celle qui se demande si ce border line vérifie les lois , définitions , formules et théorèmes , et dans la négative , par quelles modélisations astucieuses on peut l'y contraindre .
Ma culture du vide se résume à ses utilisations classiques en topologie et théorie de la mesure (tribus) , ou dans quelques démonstrations par l'absurde dans lesquelles on suppose qu'il existe ...et une anecdote:
Dieu créa le nombre entier , le reste est l'œuvre de l'homme (Kronecker) , la théorie des ensembles aussi:

,
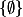
, [tex]\{Je n'ai moi même jamais reçu l'aspect juridique de la culture du vide , c'est à dire celle qui se demande si ce border line vérifie les lois , définitions , formules et théorèmes , et dans la négative , par quelles modélisations astucieuses on peut l'y contraindre .
Ma culture du vide se résume à ses utilisations classiques en topologie et théorie de la mesure (tribus) , ou dans quelques démonstrations par l'absurde dans lesquelles on suppose qu'il existe ...et une anecdote:
Dieu créa le nombre entier , le reste est l'œuvre de l'homme (Kronecker) , la théorie des ensembles aussi:
