Série de Taylor
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
DioAlex
- Messages: 8
- Enregistré le: 20 Oct 2019, 14:11
-
 par DioAlex » 22 Nov 2019, 09:14
par DioAlex » 22 Nov 2019, 09:14
Bonjour, j'ai un problème avec un exercice de maths dont l'énoncé est le suivant

, après plusieurs recherches sur les séries de Taylor je ne parviens pas à comprendre leur fonctionnement. Ici, je ne comprends pas ce qu'on veut dire par "évaluer la racine carrée de 3" et c'est ce qui me pose problème.
Je vous remercie pour votre attention et j'espère que vous pourrez m'aider

-
GaBuZoMeu
- Habitué(e)
- Messages: 6134
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 22 Nov 2019, 09:47
par GaBuZoMeu » 22 Nov 2019, 09:47
L'énoncé est assez farfelu. Pourquoi
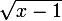
autour de
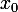
et pourquoi pas
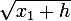
autour de 0 (avec
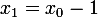
et
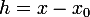
) ???
Moi je partirais de
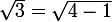
et de
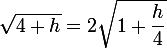
.
-
tournesol
- Membre Irrationnel
- Messages: 1509
- Enregistré le: 01 Mar 2019, 18:31
-
 par tournesol » 22 Nov 2019, 10:48
par tournesol » 22 Nov 2019, 10:48
On peut aussi poser
=\sqrt{x})
puis calculer
=\frac{1}{2\sqrt{x}})
,
=-\frac{1}{4x\sqrt{x}})
, et enfin
}(x)=\frac{3}{8x^2\sqrt{x}})
En déduire f(4)=2 ,
=\frac{1}{4})
,
=-\frac{1}{32})
et enfin
}(4)=\frac{3}{256})
Approximer

par la série de taylor en 4 :
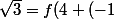)\approx f(4)+(-1)f'(4)+\frac{(-1)^2}{2!}f"(4)+\frac{(-1)^3}{3!}f^{(3)}(4)=...=1,7324...)

-
anthony_unac
- Habitué(e)
- Messages: 1116
- Enregistré le: 29 Juin 2007, 23:31
-
 par anthony_unac » 22 Nov 2019, 15:41
par anthony_unac » 22 Nov 2019, 15:41
Salut en reprenant l'idée de tournesol, tu peux choisir de travailler avec
=f(1+2))
ce qui permet de ne pas se fouler pour le calcul de f(1), f'(1), f''(1) etc ...
-
tournesol
- Membre Irrationnel
- Messages: 1509
- Enregistré le: 01 Mar 2019, 18:31
-
 par tournesol » 22 Nov 2019, 16:20
par tournesol » 22 Nov 2019, 16:20
Surtout pas car les puissances de 2 grèvent la précision .A l'ordre 3 , on obtient :
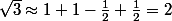
. No comment .
-
GaBuZoMeu
- Habitué(e)
- Messages: 6134
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 22 Nov 2019, 16:23
par GaBuZoMeu » 22 Nov 2019, 16:23
Hum hum, faire
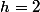
n'est pas trop top pour assurer la convergence du développement en série de
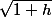
:
- Code: Tout sélectionner
h=var('h')
T=sqrt(1+h).series(h==0,10)
print T.subs(h=2).n(15)
Tbis=sqrt(1+h).series(h==0,11)
print Tbis.subs(h=2).n(15)
Réponse :
5.234
-4.262
Magnifiques approximations de la racine carrée de 2, n'est-ce pas ?


-
anthony_unac
- Habitué(e)
- Messages: 1116
- Enregistré le: 29 Juin 2007, 23:31
-
 par anthony_unac » 22 Nov 2019, 16:33
par anthony_unac » 22 Nov 2019, 16:33
Mince, j'ai commis une erreur sur le choix de h. Quelle est la valeur optimal de h pour assurer la convergence ? Que signifie n(15) dans ton code ?
-
tournesol
- Membre Irrationnel
- Messages: 1509
- Enregistré le: 01 Mar 2019, 18:31
-
 par tournesol » 22 Nov 2019, 16:37
par tournesol » 22 Nov 2019, 16:37
x=3 et h=0 .

-
anthony_unac
- Habitué(e)
- Messages: 1116
- Enregistré le: 29 Juin 2007, 23:31
-
 par anthony_unac » 22 Nov 2019, 16:39
par anthony_unac » 22 Nov 2019, 16:39
Et en prenant h=-1, ça ne part pas dans les choux ? Pourtant c'est éloigné de h=0
-
GaBuZoMeu
- Habitué(e)
- Messages: 6134
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 22 Nov 2019, 16:42
par GaBuZoMeu » 22 Nov 2019, 16:42
GaBuZoMeu a écrit:Moi je partirais de
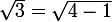
et de
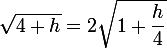
.
Pour
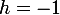
, on est à l'aise avec
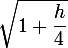
!
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 22 Nov 2019, 17:06
par Skullkid » 22 Nov 2019, 17:06
Bonjour,
Pour te donner un peu plus de détails, anthony_unac, si tu cherches à approcher
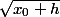
en tronquant la série de Taylor en

, tu es certain d'aller dans le mur si
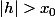
(la série diverge). Si
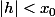
, la série converge et ton approximation sera d'autant plus efficace que
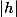
est petit devant

. Ici la réponse attendue est très probablement
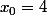
et
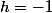
, mais un élève facétieux pourrait par exemple choisir
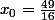
et
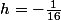
.

-
anthony_unac
- Habitué(e)
- Messages: 1116
- Enregistré le: 29 Juin 2007, 23:31
-
 par anthony_unac » 22 Nov 2019, 17:16
par anthony_unac » 22 Nov 2019, 17:16
Merci Skullkid pour ce complément d'info. Le dernier exemple que tu donnes est particulièrement astucieux et j'imagine que la "vitesse de convergence" de ce dernier n'en est que meilleur.
Modifié en dernier par
anthony_unac le 22 Nov 2019, 17:31, modifié 1 fois.
-
tournesol
- Membre Irrationnel
- Messages: 1509
- Enregistré le: 01 Mar 2019, 18:31
-
 par tournesol » 22 Nov 2019, 17:21
par tournesol » 22 Nov 2019, 17:21
Joli Skullkid .Il fallait penser aux rationnels .
-
tournesol
- Membre Irrationnel
- Messages: 1509
- Enregistré le: 01 Mar 2019, 18:31
-
 par tournesol » 22 Nov 2019, 17:46
par tournesol » 22 Nov 2019, 17:46
Skullkid , c'est plus que joli .
Avec ta methode , la precision a l'ordre 1 est meilleure que la precision a l'ordre 3 avec -1 .
On peut generaliser a l'ordre 1 en utilisant
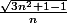
, n etant tel que
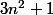
est un carre .
par exemple pour n=26 , la précision est de
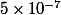
Et en plus le procédé fourni des approximations rationnelles simples de

-
DioAlex
- Messages: 8
- Enregistré le: 20 Oct 2019, 14:11
-
 par DioAlex » 23 Nov 2019, 09:54
par DioAlex » 23 Nov 2019, 09:54
Merci beaucoup pour vos réponses, je dois avouer que nous n'avons pas pour habitude d'utiliser h avec les séries de Taylor mais bien x et x0. Nous avons depuis reçu les réponses de l'exercice qui étaient x = 4 et x0 = 2, j'ai alors essayé de trouver comment arriver à la valeur x0 = 2 mais je n'ai pas encore vraiment compris le procédé.
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 23 Nov 2019, 17:00
par Skullkid » 23 Nov 2019, 17:00
Si tes notations

et

correspondent à la série de Taylor
^n}{n!}f^{(n)}(x_0))
alors ça ne va pas : prendre
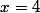
et
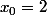
donne une série divergente, la même que celle évaluée par tournesol et GaBuZoMeu vers le début du thread.
-
DioAlex
- Messages: 8
- Enregistré le: 20 Oct 2019, 14:11
-
 par DioAlex » 24 Nov 2019, 14:26
par DioAlex » 24 Nov 2019, 14:26
C'est bien à cette série de Taylor que le x et x0 correspondent, et les valeurs x = 4 et x0 = 2 sont les valeurs réponse de l'exercice.
Ce que je ne comprends pas vraiment dans ce thème des séries de Taylor c'est, comment fait-on pour trouver le x0 le plus adéquat pour approximer une valeur de la fonction ? C'est vraiment une notion qui reste floue pour moi.
-
GaBuZoMeu
- Habitué(e)
- Messages: 6134
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 25 Nov 2019, 09:06
par GaBuZoMeu » 25 Nov 2019, 09:06
Tu n'as visiblement pas compris le corrigé donné. Si tu veux de l'aide, il faudrait transcrire des choses plus précises sur ce qui t'a été dit.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 41 invités
 , après plusieurs recherches sur les séries de Taylor je ne parviens pas à comprendre leur fonctionnement. Ici, je ne comprends pas ce qu'on veut dire par "évaluer la racine carrée de 3" et c'est ce qui me pose problème.
, après plusieurs recherches sur les séries de Taylor je ne parviens pas à comprendre leur fonctionnement. Ici, je ne comprends pas ce qu'on veut dire par "évaluer la racine carrée de 3" et c'est ce qui me pose problème.
