Critère de Cauchy, limite de fonction

[OrsayMPI]

Bonsoir à tous !

Alors voilà je bute sur le critère de Cauchy d'existence d'une limite d'une fonction.
J'ai à peu près compris le critère mais je ne vois pas du tout comment l'utiliser, il n'y a aucun exemple dans mon livre :/.

Quelqu'un pourrait par exemple me montrer comment on pourrait l'utiliser pour montrer que f(x) = 3x + 2 tend vers une limite finie quand x tend vers 0 ?

Je vous remercie d'avance !

[chan79]

Bonsoir à tous !

Alors voilà je bute sur le critère de Cauchy d'existence d'une limite d'une fonction.
J'ai à peu près compris le critère mais je ne vois pas du tout comment l'utiliser, il n'y a aucun exemple dans mon livre :/.

Quelqu'un pourrait par exemple me montrer comment on pourrait l'utiliser pour montrer que f(x) = 3x + 2 tend vers une limite finie quand x tend vers 0 ?

Je vous remercie d'avance !

salut
on se donne >0
|f(x)-f(0)|=|3x+2-2|=3|x|
si alors
le critère est vérifié et f admet une limite en 0

[mr_pyer]

Je veux bien l'appliquer à ton exemple même si là il n'y a vraiment pas besoin !! (fonction continue définie en 0)
Montrons que :
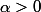
Soit , cherchons tel que si alors .
Posons , alors si ...

[jlb]

pour >0, je prends alors pour x,y réels tels que |x|< et |y|<, on a
|f(x)-f(y)|=3|x-y|<3|x|+3|y|<

[mr_pyer]

pour >0, je prends alors pour x,y réels tels que |x|< et |y|<, on a
|f(x)-f(y)|=3|x-y|<3|x|+3|y|<

Ah j'ai toujours du mal avec le vocabulaire, le critère de Cauchy c'est pas ce que j'ai écris en effet :marteau:

[OrsayMPI]

Merci beaucoup à vous deux ! C'est pas grave mr_pyer, je te remercie d'avoir prie le temps de répondre :)

[OrsayMPI]

Comment avez - vous trouvé alpha = ;)/6 ?

Quand je pose | f(x) - f(y) | < ;) en calculant je parviens à | x - y | < ;)/2 mais je ne trouve pas comment je pourrais séparer | x | et | y |. L'inégalité triangulaire ne fonctionne pas ici, car on ne connaît pas l'ordre entre |x| + |y| et ;) non ?