CPGE - dérivabilité symétriquement, K-ev ..

par **klemman** » 16 Avr 2006, 13:50

bonjour à tous

par **yos** » 16 Avr 2006, 14:30

c'est à mettre dans la rubrique lycée.

par **klemman** » 16 Avr 2006, 14:38

Ben je suis en CPGE TSI, je ne sais pas si ces choses sont vues au programme de section scientifique, ce qui doit être le cas au vu de ta remarque.

Mais c'est au programme CPGE TSI, donc voilà, j'attend votre aide :id:

par **yos** » 16 Avr 2006, 14:58

.
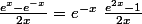
En posant X=2x, le second facteur est une forme connue :

.
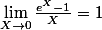
D'où la limite du produit.
Si tu connais les développements limités, tu peux aussi faire un DL1 de l'exponentielle.

par **klemman** » 16 Avr 2006, 15:14

Je n'ai pas encore vu les développements limités, mais je vais essayer de faire avec ça.

A chaque fois, il y a un petit bidouillage à faire pour connaitre la limite ?

par **yos** » 16 Avr 2006, 17:13

klemman a écrit:A chaque fois, il y a un petit bidouillage à faire pour connaitre la limite ?

petit en effet : la solution que je t'ai donnée est du niveau de terminale S.

par **Mikou** » 16 Avr 2006, 17:32

la regle de l'Hôpital donne le resultat tt aussi facilement :happy3:

par **klemman** » 16 Avr 2006, 19:14

Yos t'as fini de me rabaisser à chaque fois ? J'ai pas prétendu être bon en maths ou alors avoir un niveau supérieur que celui de Tle S.

Je demande seulement un peu d'aide.

Pour la fonction f(x) = |x|, comment pui-je partir ?

Mikou, quelle est donc cette méthode de l'Hopital ?

un peu d'aide pour l'exercice à la fin svp ?

Merci à vous

par **Mikou** » 16 Avr 2006, 19:45

pour les limites de formes indeterminées du type infini/infini ou 0/0 la loi de lHopital dit :

tu peux essayer ici ca marche :happy3:

par **yos** » 16 Avr 2006, 20:18

klemman a écrit:Yos t'as fini de me rabaisser à chaque fois ? J'ai pas prétendu être bon en maths ou alors avoir un niveau supérieur que celui de Tle S.

J'ai effectivement rabaissé le niveau du sujet. Ne t'identifie pas à lui.

|x| n'est pas dérivable en 0 (connu) mais elle est symétriquement dérivable (facile car (|x|-|-x|)/(2x)=0) . Tu as donc un (contre-)exemple qui montre que "symétriquement dérivable" n'entraîne pas "dérivable".

par **klemman** » 26 Avr 2006, 16:23

Comment faut-il faire pour démontrer que |x| est symétriquement dérivable en 0 ?

J'ai ( |x|-|-x| ) / 2x , et il faut déterminer si ça admet une limite finie en 0. Comment s'en sortir ?

CPGE - dérivabilité symétriquement, K-ev ..

CPGE - dérivabilité symétriquement, K-ev ..

Qui est en ligne