Dm de maths CPGE
17 messages
- Page 1 sur 1
Dm de maths CPGE
Bonjour,
Je viens vous demander votre aide pour un DM de maths qu'on m'a donné a faire avant de rentrer en prepa pour les ecoles de commerce
Il ne me reste que quelques questions a eclaicir mais pas moyen d'y arriver seule...
Je vous laisse y jeter un oeil:
Soit z le complexe tel que z=1+i et z' son conjugué
On pose Sn=z^n+z'^n
a) démontrer que Sn=λn cos(nπ/4) où λn est un réel a preciser en fonction de n
b) pour quelles valeurs de n a-t-on Sn=0?
c) démontrer que si n est pair, Sn est un entier relatif
On suppose que n est pair et on pose n=2m
a) écrire avec la formule du binôme les développements de (1+i)^2m et (1-i)^2m a l'aide des puissances de i
b) soit p un entier naturel. simplifier i^2p+1 + (-i)^2p+1.
simplifier i^2p + (-i)^2p
c) en deduire une écriture de S2m sous forme de somme
Merci beaucoup d'avance
Lou
Je viens vous demander votre aide pour un DM de maths qu'on m'a donné a faire avant de rentrer en prepa pour les ecoles de commerce
Il ne me reste que quelques questions a eclaicir mais pas moyen d'y arriver seule...
Je vous laisse y jeter un oeil:
Soit z le complexe tel que z=1+i et z' son conjugué
On pose Sn=z^n+z'^n
a) démontrer que Sn=λn cos(nπ/4) où λn est un réel a preciser en fonction de n
b) pour quelles valeurs de n a-t-on Sn=0?
c) démontrer que si n est pair, Sn est un entier relatif
On suppose que n est pair et on pose n=2m
a) écrire avec la formule du binôme les développements de (1+i)^2m et (1-i)^2m a l'aide des puissances de i
b) soit p un entier naturel. simplifier i^2p+1 + (-i)^2p+1.
simplifier i^2p + (-i)^2p
c) en deduire une écriture de S2m sous forme de somme
Merci beaucoup d'avance
Lou
Re: Dm de maths CPGE
Razes a écrit:Bonsoir,
a)et
On a /2 e^inπ/4 + /2-eiπ/4
apres je dois factoriser?
Re: Dm de maths CPGE
Salut,
Sachant que la définition du cosinus dans C est :
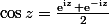
et que tu as :
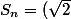^n( \rm e^{\rm i \frac{\pi}{4}n}+\rm e^{-\rm i \frac{\pi}{4}n}))
Je pense qu'ainsi c'est plus clair
Sachant que la définition du cosinus dans C est :
et que tu as :
Je pense qu'ainsi c'est plus clair
Re: Dm de maths CPGE
FLBP a écrit:Salut,
Sachant que la définition du cosinus dans C est :
et que tu as :
Je pense qu'ainsi c'est plus clair
Ca me parait plus simple avec la formule du cosinus mais je n'arrive pas a avoir la même chose que dans la question
Re: Dm de maths CPGE
Comme j'ai 2 exponentielles qui s'additionnent, je peux peut etre les factoriser?
Ce qui me gene c'est que dans la formule du cosinus j'ai un 2; alors que dans ce que j'ai j'ai deja une racine qui me gene, et 2 exponentielles qui dans leurs puissances sont eux divisés par 4...
je n'arrive pas a voir le lien avec la solution
Ce qui me gene c'est que dans la formule du cosinus j'ai un 2; alors que dans ce que j'ai j'ai deja une racine qui me gene, et 2 exponentielles qui dans leurs puissances sont eux divisés par 4...
je n'arrive pas a voir le lien avec la solution
Re: Dm de maths CPGE
J'en arrive a Sn= (/2)^n (e^ix+e^-ix)
Et je dois me retrouver avec y * e^ix+e^-ix/2
Je ne sais pas comment enlever la racine et diviser par 2 mes exponentielles
Et je dois me retrouver avec y * e^ix+e^-ix/2
Je ne sais pas comment enlever la racine et diviser par 2 mes exponentielles
Re: Dm de maths CPGE
Tu as :
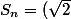^n( \rm e^{\rm i \frac{\pi}{4}n}+\rm e^{-\rm i \frac{\pi}{4}n}))
^n( \rm e^{\rm i \frac{\pi}{4}n}+\rm e^{-\rm i \frac{\pi}{4}n}))
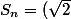^{n+2}\frac { \rm e^{\rm i \frac{\pi}{4}n}+\rm e^{-\rm i \frac{\pi}{4}n}}{2})
})
\cos {(\frac{\pi n}{4})})
Tu obtiens :
 = 2^{\frac{n+2}{2}})
Tu obtiens :
Modifié en dernier par FLBP le 29 Aoû 2017, 15:51, modifié 1 fois.
Re: Dm de maths CPGE
loubrlrd a écrit:FLBP a écrit:tu obtiens :
Je ne vois pas du tout comment
Bonjour,
Il faut savoir que :
On a donc :
Re: Dm de maths CPGE
J'ai reussi a boucler toutes les questions du 2, par contre impossible de faire les 3 dernieres questions, en commençant par celle avec la formule du Binome, help!
Re: Dm de maths CPGE
écrire avec la formule du binôme les développements de (1+i)^2m et (1-i)^2m a l'aide des puissances de i
Simple application de la formule du binôme
soit p un entier naturel. simplifier i^2p+1 + (-i)^2p+1.
i^2p+1=(i²)^p * i = (-1)^p * i
(-i)^2p+1=(-1)^p * i
donc i^2p+1 + (-i)^2p+1=2i*(-1)^p
en déduire une écriture de S2m sous forme de somme
tu calcule S2m en remplaçant z=1+i et z'=1-i
et tu utilises toutes les questions précédentes (binôme , simplification de i^2p+1 ...)
Simple application de la formule du binôme
soit p un entier naturel. simplifier i^2p+1 + (-i)^2p+1.
i^2p+1=(i²)^p * i = (-1)^p * i
(-i)^2p+1=(-1)^p * i
donc i^2p+1 + (-i)^2p+1=2i*(-1)^p
en déduire une écriture de S2m sous forme de somme
tu calcule S2m en remplaçant z=1+i et z'=1-i
et tu utilises toutes les questions précédentes (binôme , simplification de i^2p+1 ...)
17 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 36 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
