[L1] Courbes paramétrés

[benekire2]

Bonsoir,

Tout à l'heure je regardais un cours sur les courbes paramétrés et un exercice m'a interpelé,

--> Etudier la courbe [coordonnées des points de la forme (x,y)]

Alors j'ai posé x+y=t et donc on se retrouve avec et donc j'en déduis qu'il faut étudier la courbe f(t)=(x(t),y(t)) avec x(t)=t et

Je voudrais savoir si ce que j'ai fait est juste ?

Merci beaucoup :happy3:

[Ben314]

Si tu pose t=x+y, tu te retrouve avec le système :
qui, chez moi ne donne pas franchement x=t... (par contre ça donne bien )

[egan]

C'est bon pour y mais pas pour x.
Il faut bien comprendre pourquoi tu peux ramener l'étude d'une courbe à une autre. Voilà une manière de le voir:

Soit M(x;y) un point de ta courbe.
Alors
Ceci équivault successivement aux choses suivantes:
- il existe t dans R tel que t=x+y et
- il existe t dans R tel que t=x+y et
- il existe t dans R tel que et
- il existe t dans R tel que et

C'est bien l'équivalence qui te permet de faire cette étude de cette manière.

[benekire2]

D'accord , merci à vous deux. Si j'ai posé la question, c'est que je pensais effectivement être un escroc , maintenant j'en suis sûr :zen:

Donc du coup ça me donne comme egan me me suggère ,

Autre question :

Soit C la courbe d'équation polaire
Montrer qu'une droite passant par O et d'angle polaire coupe la courbe en trois points et que les tangentes en ces trois points à la courbe sont les côtés d'un triangle équilatéral.

Je n'y arrive pas trop ... désolé je commence les courbes paramétrés :--:

Merci ! :id:

[benekire2]

RE !

Finallement, j'ai réussi !

Je me suis mit dans le repère (O,u(theta),v(theta)) qui est orthonormé, et j'ai calculé avec le produit scalaire l'angle entre la tangente et u(theta) et j'ai pu conclure , ouff :we:

[Ben314]

Bon,
La "courbe d'équation polaire " (on utilise en général la lettre greque "rho" : ) c'est la courbe d'équation paramétrique : et en général on précise dans quel ensemble est .
Ici, y'a qu'a admettre c'est l'ensemble de définition de la fonction c'est à dire

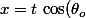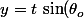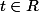
Le point est sur la "droite d'équation polaire " (i.e. d'équation paramétrique , avec ) ssi (cas à ne pas oublier dans lequel mais inutile ici vu que pour tout ) ou bien (attention, n'est pas l'équation d'une droite mais seulement d'une demi-droite)

Les correspondant aux points d'intersections ont donc pour coordonnées polaires , où doit être tel que .
A priori, il y a 6 points correspondant à k=0,1,...,5 sauf qu'en regardant mieux, et donc les points correspondant à k=0 et k=3 sont les même. Idem pour k=1 et k=4 ainsi que pour k=2 et k=5.
Il y a donc bien 3 points d'intersection a condition que , et c'est à dire à condition que c'est à dire à condition que ne soit pas l'axe des y (si est l'axe des y, il n'y a que 2 points d'intersection : )
Une deuxième condition pour qu'il y ait 3 "vrai" points d'intersection et que les 3 points soient distincts, ce qui s'avère ne pas être le cas lorsque (i.e est l'axe des x) ou il n'y a que deux points : (1,0) et (-8,0) mais (-8,0) est un point double de la courbe et il y a donc deux tangentes en ce point ce qui fait bien 3 tangentes avec celle en (1,0) (qui forment bien un triangle équilatéral).

[benekire2]

Merci de cette réponse !

En effet on utilise la courbe paramétrés définie par

définie sur

On considère la droite d'équation polaire

Et je décide de tout faire en polaire en fait ,

La droite coupe la courbe paramétré aux points de paramètres pour
Cela dit du fait que il n'y a que 3 points d'intersection, pour k=0 , k=1 et k=2. [1]

On note A l'angle que fait la tangante en avec le vecteur
On se retrouve avec ;

Et pour calculer ce produit scalaire et cette norme on se place dans le repère orthonormé

Ainsi

On trouve un résultat similaire pour

Finalement on a
i.e l'angle de la tangente qui va se trouve en M va être et donc en remplaçant par ce qu'on a trouvé en [1] on arrive au résultat :id:

Voilà :we: