Courbes Paramétrées
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
lanfranky
- Membre Naturel
- Messages: 18
- Enregistré le: 06 Déc 2014, 12:13
-
 par lanfranky » 28 Avr 2015, 07:40
par lanfranky » 28 Avr 2015, 07:40
Bonjour,
Je bloque directement à la première question d'un devoir maison sur les courbes paramétrées ...
voici l'énoncé :
On considère la courbe paramétrée (C) définie pour 0

t


/2 par:
M(t) : x(t)=sin²t
y(t)=4sint cost
1.Calculer les coordonnées du point M(;)/2-t) puis celle du milieu N(t) du segment [M(t), M(;)/2 - t)].
En déduire que (C) est symétrique par rapport çà une droite (D) qu'on pécisera.
En déduire un intervalle d'étude d'origine.
Pour mes réponses j'ai trouvé (mais le hic c'est que je sais pas si j'avance bien ...) :
M(;)/2-t) : x(;)/2-t) =sin²(;)/2-t) = sin²(t-;)/2)
y (;)/2-t) = 4sin(;)/2-t) cos(;)/2-t) =4cost sint = 4sint cost = y(t)
N(t) : X(t) = [sin²t+sin²(t-;)/2)]/2
Y(t) = [4sint cost+4sint cost]/2= 4sint cost = y(t)Donc à par dire que y(t) reste le m^me et qu'il pourrait y avoir une symétrie suivant la valuer que prend t pour x(t) , x(;)/2-t) et X(t) bin je vois pas ou ça me mène ...
Pourriez vous me débloquer SVP ?
Merci

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 28 Avr 2015, 08:36
par zygomatique » 28 Avr 2015, 08:36
salut
en posant p = pi
sin(p/2 - t) = cos(t)
donc M(p/2 - t) a pour coordonnées
cos²(t)
4sin(t)cos(t)
donc le milieu N(t) a pour coordonnées
1/2
4sin(t)cos(t)
symétrie par rapport à la droite d'équation x = 1/2
....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
mathelot
 par mathelot » 28 Avr 2015, 08:40
par mathelot » 28 Avr 2015, 08:40
bonjour,
soit

y(t')=y(t)
x(t')=1-x(t)
d'où une symétrie par rapport à la droite d'équation x=1/2
soit

y(t")=-y(t)
x(t")=x(t)
d'où une symétrie par rapport à l'axe x'Ox
soit

=y(t))
=x(t))
d'où
)
et
)
sont

-périodiques.
intervalle d'étude :
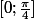
comment complète-t-on la courbe ?
remarque: ta courbe est une ellipse (ou une partie d'une ellipse)
comme on le voit en passant à l'arc double 2t
d'équation (y/2)^2+(x-1/2)^2=1pour aider au tracé,
ici
-
lanfranky
- Membre Naturel
- Messages: 18
- Enregistré le: 06 Déc 2014, 12:13
-
 par lanfranky » 28 Avr 2015, 08:57
par lanfranky » 28 Avr 2015, 08:57
merci !!!
Comme je ne savais pas si l'on pouvait dire que sin²(t)= sint*sint
et en sachant que sin(;)/2-t) = cost d'où sin²(;)/2-t)=cos(t)*cos(t)=cos²(t)
je suis passé par sin²t=(1-cos2t)/2
bon je me suis un peu beaucoup^embété mais j'ai bien trouvé xn(t)=1/2 yn(t)=yt
par contre du coup mon intervalle d'origine est bien [1/2,;)/2]?
-
mathelot
 par mathelot » 28 Avr 2015, 09:12
par mathelot » 28 Avr 2015, 09:12
l'intervalle d'étude est
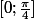
qui est envoyé sur

par

(on complète la courbe par une symétrie par rapport à la droite d'équation x=1/2)
puis par une symétrie par rapport à l'axe x'Ox pour l'avoir sur

-
mathelot
 par mathelot » 28 Avr 2015, 13:26
par mathelot » 28 Avr 2015, 13:26
-
lanfranky
- Membre Naturel
- Messages: 18
- Enregistré le: 06 Déc 2014, 12:13
-
 par lanfranky » 28 Avr 2015, 16:17
par lanfranky » 28 Avr 2015, 16:17
excusez moi mais je bloque encore ... cette fois on me demande de déterminer l'equation de (c) sous la forme y=f(x) ...
comment puis je faire ?
-
lanfranky
- Membre Naturel
- Messages: 18
- Enregistré le: 06 Déc 2014, 12:13
-
 par lanfranky » 28 Avr 2015, 16:24
par lanfranky » 28 Avr 2015, 16:24
Excuse moi mais moi y en a pas comprendre d'où sort le 2x-1=-cos2t etc etc ... lol
en plus c'est la dernière question de l'exercice...
Je ne serai pas contre un autre petit coup de main stp
merci encore !

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 28 Avr 2015, 18:15
par zygomatique » 28 Avr 2015, 18:15
lanfranky a écrit:Excuse moi mais moi y en a pas comprendre d'où sort le 2x-1=-cos2t etc etc ... lol
en plus c'est la dernière question de l'exercice...
Je ne serai pas contre un autre petit coup de main stp
merci encore !
calcule 2x - 1 ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 31 invités
