Salut tout le monde
1/
z^n/ln(n) là je crois que c'est simple z^n est bornée car suite géométrique de somme égale |1-z^n+1/1-z|<=2/|1-z|
et ln(n) décroissante vers 0 : On applique Abel donc la série converge
Mais je sens qu'il y a une erreur quelque part?
3/
))
la c'est pareil pour
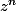
mais pour tan il n y a t il pas de méthode ou astuce intelligente a part étudier la fonction pour dire qu'elle décroit vers 0 (afin d'appliquer Abel bien sur ?)
4/
)
et
 + 1/n)
sont équivalente ? elles sont de même nature ?
Pour l'équivalence j'ai appliquer la définition ilf aut prouver en fait que
+1/n|)
à partir d'un certain rang .. mais je ne vois pas le n' :triste: je sais qu'ils ont la même limite mais je ne vois pas du tout comment faire ! :triste:
Merci de m'apporter votre aide !
