Corps de rupture et extensions...
17 messages
- Page 1 sur 1
Corps de rupture et extensions...
Bonsoir,
J'ai quelques doutes sur les corps de rupture et surtout sur ce qu'on entend par les "automorphismes" associés.
On construit le corps de rupture associé à P irréductible sur Q par:
Q(a) avec a (a racine de P)
ensuite on montre que l'autre racine est dans Q(a). Mais ensuite on me demande "combien d'automorphismes existe-t-il" et je n'ai pas compris ce qu'on me demande?
J'ai quelques doutes sur les corps de rupture et surtout sur ce qu'on entend par les "automorphismes" associés.
On construit le corps de rupture associé à P irréductible sur Q par:
Q(a) avec a (a racine de P)
ensuite on montre que l'autre racine est dans Q(a). Mais ensuite on me demande "combien d'automorphismes existe-t-il" et je n'ai pas compris ce qu'on me demande?
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Corps de rupture et extensions...
Ben pourtant c'est on ne peut plus clair : on te demande combien il y a d'automorphisme de Q[a], c'est à dire de morphisme de corps bijectif de Q[a] dans Q[a].
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Corps de rupture et extensions...
ensuite on montre que l'autre racine est dans Q(a)
comment sais-tu qu'il n'y en a que deux ?
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: Corps de rupture et extensions...
zygomatique a écrit:ensuite on montre que l'autre racine est dans Q(a)
comment sais-tu qu'il n'y en a que deux ?
. c'est un polynôme du second degré
@Ben: merci ... je vais...essayer de relire des cours
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Corps de rupture et extensions...
Ben314 a écrit:Ben pourtant c'est on ne peut plus clair : on te demande combien il y a d'automorphisme de Q[a], c'est à dire de morphisme de corps bijectif de Q[a] dans Q[a].
Par exemple Ben, si on a P = X^2 + 2X + 2, je peux dire que Q(-1-i) ainsi que Q(-1+i) est isomorphe à Q[X]/(P) ? Comme (P) idéal maximal c'est un corps?
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Corps de rupture et extensions...
il me semble bien (j'en suis sur d'ailleurs) qu'un automorphisme de Q[a] laisse fixe Q ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: Corps de rupture et extensions...
Euhhhh
Le truc c'est que à part mon isomorphisme je vois pas le format de la réponse attendu. Il faut que l'automorphisme parte de Q(a) dans Q(a). Bon je crois que mon q[X]/(P) est hors sujet?
Le truc c'est que à part mon isomorphisme je vois pas le format de la réponse attendu. Il faut que l'automorphisme parte de Q(a) dans Q(a). Bon je crois que mon q[X]/(P) est hors sujet?
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Corps de rupture et extensions...
Effectivement, les corps Q(-1-i) et Q(-1+i) sont isomorphes vu qu'ils sont tout les eux isomorphes à Q[X]/(X²+2X+2), mais on peut pas dire que ça soit d'un grand intérêt vu que :
- Je vois pas trop le rapport avec la question qu'on te pose qui est de déterminer les automorphismes de Q[X]/(X²+2X+2) dans lui même.
- Vu que) les sous corps Q(-1-i) et Q(-1+i) de C sont non seulement isomorphes mais bien plus bêtement... égaux.
les sous corps Q(-1-i) et Q(-1+i) de C sont non seulement isomorphes mais bien plus bêtement... égaux.
Sinon, comme le dit zygo (et c'est le mini du mini à savoir), un morphisme de corps F entre corps de caractéristique 0 (donc contenant Q) doit envoyer les éléments de Q sur eux même vu que par définition, on doit avoir F(0)=0 et F(1)=1, qu'on en déduit par récurrence que F(n)=n pour tout naturel n puis que F(m)=m pour tout entier relatif m puis que F(q)=q pour tout rationnel q.
Donc pour entièrement déterminer un morphisme de corps F de Q(a) dans n'importe quel autre corps, il suffit de donner la valeur de F(a). Sauf que cette valeur n'est pas quelconque...
- Je vois pas trop le rapport avec la question qu'on te pose qui est de déterminer les automorphismes de Q[X]/(X²+2X+2) dans lui même.
- Vu que
Sinon, comme le dit zygo (et c'est le mini du mini à savoir), un morphisme de corps F entre corps de caractéristique 0 (donc contenant Q) doit envoyer les éléments de Q sur eux même vu que par définition, on doit avoir F(0)=0 et F(1)=1, qu'on en déduit par récurrence que F(n)=n pour tout naturel n puis que F(m)=m pour tout entier relatif m puis que F(q)=q pour tout rationnel q.
Donc pour entièrement déterminer un morphisme de corps F de Q(a) dans n'importe quel autre corps, il suffit de donner la valeur de F(a). Sauf que cette valeur n'est pas quelconque...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Corps de rupture et extensions...
D'accord Ben, je vois...
Au risque de dire une bêtise: si je renvoie a sur l'autre racine du polynôme (F(a)=-2-a ou quelque chose), est-ce que cela peut donner un automorphisme convenable?
Au risque de dire une bêtise: si je renvoie a sur l'autre racine du polynôme (F(a)=-2-a ou quelque chose), est-ce que cela peut donner un automorphisme convenable?
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Corps de rupture et extensions...
Ben oui.
Et c'est le B-A-BA de ce qui concerne les morphismes de corps :
Si tu as des éléments d'un corps
d'un corps  tels que
tels que  et un morphisme de corps
et un morphisme de corps  alors tu doit évidement avoir
alors tu doit évidement avoir \!+\!\varphi(a_1)\varphi(x)\!+\!...\!+\!\varphi(a_n)\varphi(x)^n\!=\!0_{k'}) .
.
Et celà signifie que, si tu connait déjà les images de par
par  et que tu cherche les images possibles pour
et que tu cherche les images possibles pour  , ben faut que ce soit une des racines dans
, ben faut que ce soit une des racines dans 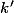 du polynôme
du polynôme \!+\!\varphi(a_1)X\!+\!...\!+\!\varphi(a_n)X^n) .
.
Et cet truc là qui semble totalement stupide tellement c'est évident, ben c'est en fait la "clef de voute" de la théorie de Galois vu que ça te dit que si tu as un automorphisme F d'un corps k (de caractéristique nulle) et un polynôme P à coeff. dans Q qui a ces racines dans k alors ton automorphisme F envoie les racines de P sur des racines de P et comme tout morphisme de corps est injectif, c'est que F permute les racines de P et que ça permet d'associer à F un élément du groupe des permutation (de l'ensemble des racines de P).
Bon, sinon pour revenir à l'exo lui même, si est un automorphisme de Q(a), il est forcément égal à l'identité sur Q et, comme
est un automorphisme de Q(a), il est forcément égal à l'identité sur Q et, comme  , on doit avoir
, on doit avoir
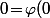\!=\!\varphi(a^2\!+\!2a\!+\!2)\!=\!\varphi(a)^2\!+\!\varphi(2)\varphi(a)\!+\!\varphi(2)\!=\!\varphi(a)^2\!+\!2\varphi(a)\!+\!2) vu que
vu que  .
.
Donc) doit être racine du polynôme
doit être racine du polynôme  ce qui ne laisse que deux possibilités :
ce qui ne laisse que deux possibilités :
- Soit\!=\!a) et
et  c'est l'identité (on devait forcément la trouver parmi les solution celle là !!!)
c'est l'identité (on devait forcément la trouver parmi les solution celle là !!!)
- Soit\!=\!-2\!-\!a\!=\!\frac{2}{a}) qui est l'autre racine du polynôme et qui est bien elle aussi un élément de Q(a).
qui est l'autre racine du polynôme et qui est bien elle aussi un élément de Q(a).
Si tu ne connais aucune théorie pour le moment, vérifie "à la main" que cette égalité\!=\!-2\!-\!a) définie bien un unique morphisme de corps sur Q(a).
définie bien un unique morphisme de corps sur Q(a).
Indication : Il est complètement inutile, voire même nocif à la compréhension, de calculer explicitement la valeur de et de même, plutôt que d'écrire
et de même, plutôt que d'écrire \!=\!-2\!-\!a) , il vaut bien mieux écrire
, il vaut bien mieux écrire \!=\!a') où
où 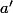 est une des racines de
est une des racines de  .
.
L'écriture sert uniquement et exclusivement à montrer que
sert uniquement et exclusivement à montrer que 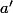 est bien un élément de Q(a).
est bien un élément de Q(a).
Et c'est le B-A-BA de ce qui concerne les morphismes de corps :
Si tu as des éléments
Et celà signifie que, si tu connait déjà les images de
Et cet truc là qui semble totalement stupide tellement c'est évident, ben c'est en fait la "clef de voute" de la théorie de Galois vu que ça te dit que si tu as un automorphisme F d'un corps k (de caractéristique nulle) et un polynôme P à coeff. dans Q qui a ces racines dans k alors ton automorphisme F envoie les racines de P sur des racines de P et comme tout morphisme de corps est injectif, c'est que F permute les racines de P et que ça permet d'associer à F un élément du groupe des permutation (de l'ensemble des racines de P).
Bon, sinon pour revenir à l'exo lui même, si
Donc
- Soit
- Soit
Si tu ne connais aucune théorie pour le moment, vérifie "à la main" que cette égalité
Indication : Il est complètement inutile, voire même nocif à la compréhension, de calculer explicitement la valeur de
L'écriture
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Corps de rupture et extensions...
Merci Ben, j'ai compris.
Par curiosité de quelle "théorie" tu parles? La vérification que c'est un morphisme de corps est évidente non?
Le mot "unique" est un peu ... flou?
Ben314 a écrit:Si tu ne connais aucune théorie pour le moment, vérifie "à la main" que cette égalitédéfinie bien un unique morphisme de corps sur Q(a).
Par curiosité de quelle "théorie" tu parles? La vérification que c'est un morphisme de corps est évidente non?
Le mot "unique" est un peu ... flou?
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Corps de rupture et extensions...
Ben "la théorie", ici, c'est de savoir que si P est un polynôme irréductible sur un corps k mais qui admet une racine alpha dans un surcorps K de k, alors le corps k[X]/(P) est isomorphe au sous corps k[alpha] de K via le passage au quotient de l'application Q->Q(alpha) de k[X] dans K (qui a comme noyau l'idéal (P) de k[X]).
Et ça, ça te vend quasi direct que si beta est une autre racine de P dans K alors les sous-corps k[alpha] et k[beta] de K sont isomorphes via un unique morphisme alpha->beta.
Et ça, ça te vend quasi direct que si beta est une autre racine de P dans K alors les sous-corps k[alpha] et k[beta] de K sont isomorphes via un unique morphisme alpha->beta.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Corps de rupture et extensions...
D'accord...
Un autre exemple: un polynôme ayant pour racines
(exp(2ipi/9) ; exp(4ipi/9); exp(8ipi/9) ; - exp(ipi/9); - exp(5ipi/9), - exp(7ipi/9))
J'ai l'impression qu'on peut renvoyer les 3 premières les unes sur les autres et les trois dernières. Je me trompe?
Un autre exemple: un polynôme ayant pour racines
(exp(2ipi/9) ; exp(4ipi/9); exp(8ipi/9) ; - exp(ipi/9); - exp(5ipi/9), - exp(7ipi/9))
J'ai l'impression qu'on peut renvoyer les 3 premières les unes sur les autres et les trois dernières. Je me trompe?
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Corps de rupture et extensions...
Ben, déjà, il faudrait que tu précise le contexte : tu ta place dans quel corps ?
Dans celui engendré (sur Q) par ces 6 éléments là ?
Dans celui engendré (sur Q) par ces 6 éléments là ?
Modifié en dernier par Ben314 le 31 Déc 2016, 01:49, modifié 2 fois.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Corps de rupture et extensions...
Oui c'est à dire que je regarde les extensions Q(exp(i pi...) )
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Corps de rupture et extensions...
Le corps K en question est en fait engendré par n'importe lequel des 6 éléments qui sont les 6 racines du polynôme cyclotomique d'ordre 9 (qui est irréductible sur Q).
Et comme K est engendré par un unique élément (parmi les 6), il suffit de se donner l'image de cet élément pour entièrement déterminer un unique automorphisme de K. Et concernant cette image, ben tu peut prendre n'importe lequel des 6 éléments (si tu reprend le même, ça fait l'identité, si tu prend le conjugué de celui de départ, ça te donne l'application de conjugaison)
Bref, dans ce cas, l'ensemble des automorphismes de K est un groupe isomorphe à Z/6Z.
Et comme K est engendré par un unique élément (parmi les 6), il suffit de se donner l'image de cet élément pour entièrement déterminer un unique automorphisme de K. Et concernant cette image, ben tu peut prendre n'importe lequel des 6 éléments (si tu reprend le même, ça fait l'identité, si tu prend le conjugué de celui de départ, ça te donne l'application de conjugaison)
Bref, dans ce cas, l'ensemble des automorphismes de K est un groupe isomorphe à Z/6Z.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Corps de rupture et extensions...
Ben314 a écrit:Le corps K en question est en fait engendré par n'importe lequel des 6 éléments qui sont les 6 racines du polynôme cyclotomique d'ordre 9 (qui est irréductible sur Q).
 tu es trop fort
tu es trop fort Merci pour ton aide Ben ! Je vais regarder tout cela à tête reposé et je reviendrai demain avec d'autres questions... merci beaucoup pour ton aide, sans toi je ne m'en sortirais jamais.
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
17 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 50 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
