Convergence de suite de matrices

[elvis77]

Bonsoir,

Je voudrais savoir comment montrer proprement et en détails le fait suivant. Soit une matrice M dans Mn(C) et on fait la décomposition de Dunford : M=D+N sous de bonnes hypothèses (ma question fait partie d'une démonstration plus grande) j'obtiens : Pour X dans C^n

On en conclut que n'est pas borné dans C^n.
Je sens bien que le fait de faire tendre p vers + l'infini va faire fonctionner le truc mais je n'arrive pas à l'écrire correctement, j'ai essayé de minoré ma suite (avec une norme) par quelque chose qui ne dépend que de p mais je bloque.
Merci pour votre aide,
Bien cordialement.

[Ben314]

Salut,
Je comprend pas grand chose à tes arguments :
- Pourquoi n'as tu que deux termes dans le développement de (D+N)^p ? La matrice N est certes nilpotente, mais ça ne veut pas dire que N^2=0.
- Je ne vois aucune raison particulière d'en "conclure que M^pX est non bornee".

Sinon, comme Mn (C) est de dimension finie, toutes les normes sont équivalente dessus et pour montrer un truc topologique (par exemple une convergence) ben on prend la norme la plus adaptée au problème. Sauf que là, vu que je comprend pas le problème c'est pas gagné . . . (c'est quoi le"truc" que tu voudrait faire fonctionner ?)

[elvis77]

Merci pour votre réponse.
Le thème du problème est d'étudier les petits sous-groupes de GLn(C), la référence : Francinou Algèbre 2 ex 3.9
On suppose que c'est pour cela qu'on a l'égalité puis Francinou nous dit "il en découle que n'est pas bornée dans C^n".
Argument supplémentaire : on sait que toutes les valeurs propres de M sont de modules 1. (cela peut-il aider?)
Merci,
Cordialement.

[elvis77]

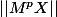
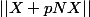
Peut-être une idée : est ce que les valeurs propres de M sont les mêmes que D? SI oui alors quand on fait tendre p vers l'infini on a qui "tend vers" et ensuite comment écrire que n'est pas bornée ?
Merci.

[Ben314]

Déjà, les valeurs propres de M sont évidement celle de D.
Sinon, D^(p-1) est une matrice diagonale dont les termes de la diagonale sont de module =1 donc le max (en module) des coordonnées de D^(p-1)NX c'est toujours le même que celui de NX qui est non nul. Et en multipliant par p, ben ça tend vers l'infini alors que l'autre terme de la somme à des coordonnées qui restent bornées
Donc le vecteur M^pX a au moins une de ces coordonnées qui tend vers l'infini (en module) ce qui prouve évidement qu'une des coordonnés de la matrice M^p tend vers l'infini.

[elvis77]

Merci beaucoup !