Convergence en mesure
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Cryptocatron-11
- Membre Rationnel
- Messages: 604
- Enregistré le: 18 Déc 2010, 22:19
par Cryptocatron-11 » 27 Oct 2012, 15:20
Bonjour,
On considère la mesure de Lebesgue sur l'intervalle [0,1].
Soit
 = 1)
pour
, 0 ailleurs
où n est un en entier tel que :
}{2} \leq k \leq \frac{n(n+1)}{2})
et
}{2})
)
converge en mesure vers 0. En effet,
:
 | \geq \epsilon \} \leq \frac{1}{n} \ ->0)
quand
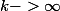
Dans le livre, il est rajouté "
Cependant il n'y a convergence en aucun point de l'intervalle [0,1]. "
Est ce qu'il parle seulement de la convergence uniforme (auquel cas je comprendrai) ? Car il y a ici convergence simple sur [0,1] , non ?
-
Arkhnor
- Membre Relatif
- Messages: 343
- Enregistré le: 05 Déc 2008, 22:02
par Arkhnor » 27 Oct 2012, 16:01
Bonjour,
Est ce qu'il parle seulement de la convergence uniforme (auquel cas je comprendrai) ? Car il y a ici convergence simple sur [0,1] , non ?
Non. Pourquoi ? Que vaut
)
par exemple ?
Essaye de visualiser le graphe de
et comment il évolue quand
va à l'infini.
-
Cryptocatron-11
- Membre Rationnel
- Messages: 604
- Enregistré le: 18 Déc 2010, 22:19
par Cryptocatron-11 » 27 Oct 2012, 17:21
Pour les premiers termes on aura :
 = 1)
pour
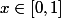
, 0 ailleurs
 = 1)
pour
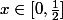
, 0 ailleurs
 = 1)
pour
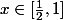
, 0 ailleurs
 = 1)
pour
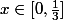
, 0 ailleurs
 = 1)
pour
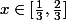
, 0 ailleurs
 = 1)
pour
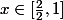
, 0 ailleurs
et ainsi de suite... Et on voit que lorsque k va tendre vers l'infini, ben
vaudra 1 sur un intervalle infiniment petit.
Quant à la valeur
)
:
Quand n tend vers l'infini, ça ne converge pas car ça fait un coup 1 et un coup 0
-
Arkhnor
- Membre Relatif
- Messages: 343
- Enregistré le: 05 Déc 2008, 22:02
par Arkhnor » 27 Oct 2012, 18:03
Donc ça ne converge pas simplement vers 0. (le même raisonnement vaut d'ailleurs pour f_n(x), et pas seulement pour f_n(0), ce qui entraine que l'on a pas non plus la convergence presque sure)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 31 invités
