Convergence et limite de suite

par **Ptiboudelard** » 12 Jan 2010, 20:01

Bonsoir !

Voilà, j'ai un petit souci, car trou de mémoire... Je ne me souviens plus comment prouver la convergence dans ce type d'exercice ( qui je suis sûr est simplissime ... mais je n'ai pas touché aux suites depuis un bout de temps )

on a la suite

définie par son premier terme

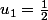
et la relation de récurrence suivante :

Montrer que la suite

est convergent et trouver sa limite ...

par **Ben314** » 12 Jan 2010, 20:04

Bonsoir,
Perso, dans ce genre d'exercice, je commence systématiquement par écrire : si la suite admet une limite L alors cette limite doit vérifier...
Ca permet de "cerner" le problème et donne des indicateurs sur qui sont des majorants/minorant possibles...

par **Ptiboudelard** » 12 Jan 2010, 20:04

d'accord, je tente :-D

par **Ptiboudelard** » 12 Jan 2010, 20:09

En fait je l'avais déjà fait, mais je ne vois pas trop où ca mène ... :

Supposons

convergente, alors on a

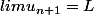
d'où on a aussi,

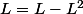
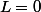
Mais ce ne sont que des suppositions ... c'est ca le problème ... non ? :-S

par **sniperamine** » 12 Jan 2010, 20:10

Ptiboudelard a écrit:En fait je l'avais déjà fait, mais je ne vois pas trop où ca mène ... :

Supposons convergente, alors on a

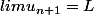
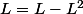
d'où on a aussi, L=0

Mais ce ne sont que des suppositions ... c'est ca le problème ... non ? :-S

oui des suppositions pour prévoir un peu la procédure !!

par **Ptiboudelard** » 12 Jan 2010, 20:11

oui mais du coup, comment affirmer ?

par **sniperamine** » 12 Jan 2010, 20:19

Ptiboudelard a écrit:oui mais du coup, comment affirmer ?

tu peux pas affirmer tu dois voir si ta suite croissante majorée ou si elle décroissante ou minorée et là tu peux affirmer qu'elle admet une limite !!

par **Ptiboudelard** » 12 Jan 2010, 20:21

je suis d'accord, on voit directement qu'elle est décroissante car on a :

soit

or

d'où

décroissante... Mais c'est le minorant que je n'arrive pas à trouver ...

par **Ptiboudelard** » 12 Jan 2010, 20:24

le minorant serait il 0, en vertu de ce que l'on a trouvé pour l ?

par **sniperamine** » 12 Jan 2010, 20:28

Ptiboudelard a écrit:le minorant serait il 0, en vertu de ce que l'on a trouvé pour l ?

essaies d'étudier la fonction x___>-x²+x et tu verras !!

par **Doraki** » 12 Jan 2010, 20:30

Oui on peut montrer sans trop de mal que 0 est un minorant.

par **Ptiboudelard** » 12 Jan 2010, 20:34

sniperamine : je ne vois pas où tu veux en venir je suis désolé ... peux tu être plus exhaustif ? J'ai étudié la fonction, j'ai trouvé croissante --- 1/2 ---- décroissante... et la limite en +oo est -oo

par **sniperamine** » 12 Jan 2010, 20:37

Ptiboudelard a écrit:sniperamine : je ne vois pas où tu veux en venir je suis désolé ... peux tu être plus exhaustif ? J'ai étudié la fonction, j'ai trouvé croissante --- 1/2 ---- décroissante... et la limite en +oo est -oo

ah ok ça n'a rien donné donc tu montres que 0 est un minorant tout simplement puisque la suite décroit vers sa limite !!

par **Ptiboudelard** » 12 Jan 2010, 20:39

oui donc en gros, on a a trouvé ( en supposant que la suite était convergente ) que L= 0

de plus U_n décroissante donc U_n convergente et sa limite est L=0 ?

par **Ptiboudelard** » 12 Jan 2010, 20:40

Ca me parait un peu bancal car je trouve que beaucoup de choses ne sont pas vérifiées ... on suppose ...

par **sniperamine** » 12 Jan 2010, 20:42

Ptiboudelard a écrit:oui donc en gros, on a a trouvé ( en supposant que la suite était convergente ) que L= 0

de plus U_n décroissante donc U_n convergente et sa limite est L=0 ?

ben le fait de calculer l'éventuelle limite te donne seulement des idées pour trouver un éventuel minorant majorant mais tu dois vérifier les hypothèses de convergence c'est tout

par **Doraki** » 12 Jan 2010, 20:43

D'abord on montre que la suite est minorée par quelque chose.
Ensuite on en déduit que comme elle est décroissante, elle est forcément convergente vers quelque chose.
Une fois qu'on sait qu'elle est convergente, on sait qu'elle converge vers 0.

Convergence et limite de suite

Convergence et limite de suite

Qui est en ligne