Convergence absolue d'une série de fonction

[Wenneguen]

Bonjour,

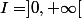
je dois étudier la convergence uniforme de la série de fonctions sur en m'aidant d'une comparaison série intégrale.
Apparemment la réponse c'est qu'elle ne converge pas uniformément mais je n'arrive pas à le montrer.

Un peu d'aide serait la bienvenue, merci !

[cuati]

Bonjour,
pourquoi à l'aide d'une comparaison série intégrale ? Il est assez évident qu'elle ne vérifie pas le critère de Cauchy uniforme sur I...

[Doraki]

Pour contredire la convergence uniforme, tu dois trouver un ;) (disons ;)=1, dans ton cas, n'importe lequel convient) tel que pour tout n0 il existe un x tel que la série pour n >= n0 de f(n,x) dépasse ;), c'est à dire il existe n1 >= n0 tel que la somme pour n0 <= n <= n1 de f(n,x) >= 1 :

Pour tout n0 il existe x (proche de 0) et n1 (grand) tel que la somme pour n0<=n<=n1 des f(n,x) >= 1.

Le truc c'est de choisir n1 avant de choisir x, et d'étudier à n0 et n1 fixés la limite quand x tend vers 0 des sommes finies, qui existe toujours, et que tu peux estimer en comparant avec une intégrale.

[Maxmau]

Bonjour,

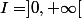
je dois étudier la convergence uniforme de la série de fonctions sur en m'aidant d'une comparaison série intégrale.
Apparemment la réponse c'est qu'elle ne converge pas uniformément mais je n'arrive pas à le montrer.

Un peu d'aide serait la bienvenue, merci !

Bj
S(x) la somme de la série
Sn(x) la somme partielle
Ln la limite de Sn(x) pour x tendant vers 1 par valeurs supérieures

Si l'on traduit la CU de la série sur I=]1, +inf[ à l'aide du critère de cauchy, on a:
pour tout e >0, il existe un rang N tq (p,q>N) implique ( pour tout x de I |Sp(x) - Sq(x)| 0, il existe un rang N tq (p,q>N) implique ( |Lp - Lq| <= e )
donc (Ln) est une suite de cauchy
A toi de conclure

ps: On peut aussi faire ce raisonnement par l'absurde en utilisant un résultat classique de permutation de limites

[Wenneguen]

On a pas vu ce critère en cours :/

[Wenneguen]

Pour contredire la convergence uniforme, tu dois trouver un (disons =1, dans ton cas, n'importe lequel convient) tel que pour tout n0 il existe un x tel que la série pour n >= n0 de f(n,x) dépasse , c'est à dire il existe n1 >= n0 tel que la somme pour n0 = 1 :

Pour tout n0 il existe x (proche de 0) et n1 (grand) tel que la somme pour n0= 1.

Le truc c'est de choisir n1 avant de choisir x, et d'étudier à n0 et n1 fixés la limite quand x tend vers 0 des sommes finies, qui existe toujours, et que tu peux estimer en comparant avec une intégrale.

Cette version en français m'embrouille un peu, tu pourrais me l'écrire avec des et des stp ? ^^

[Doraki]

La négation de la convergence uniforme est :

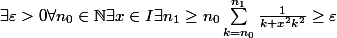
[cuati]

Oui, bon, c'est la négation du critère de Cauchy uniforme...