La continuité uniforme

[Anonyme]

Bonjour
Est-ce que vous pouvez m'expliquer les étapes à suivre (en détail) pour résoudre un exercice sur la continuité uniforme comme par exemple celui ci :

g(x) = x+sin(x) , avec x appartenant à R.

Merci de votre aide.

[abcd22]

Ici ce n'est pas difficile de montrer la continuité uniforme : g'(x) = 1 + cos x, g' est bornée donc avec l'inégalité des accroissements finis on trouve que g est lipschitzienne donc uniformément continue.

[Anonyme]

merci pour ton aide . mais est ce que tu peux m'éclairer un peu plus.

[abcd22]

La dérivée est bornée par 2, donc l'inégalité des accroissements finis donne pour tous x et y réels (g est 2-lipschitzienne). Si on prend 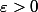, dès que , . La fonction est donc uniformément continue (le r ne dépend que du , pas de x et y). Toutes les fonctions dérivables dont la dérivée est bornée sont uniformément continues, avec la même démonstration qu'ici.

[Anonyme]

merci à toi ABCD22 , j'ai bien compris . je voulais vs demandez est ce que vs pouvez m'expliquer cette énoncé : on ns demande de voir si ces fonction sont uniformément continue : f(x) = racine de x , avec x apartenant à [0 , +00[
et g(x) = 1/x , avec x apartenant à ]0,1] . merci pour ton aide .

[abcd22]

Racine de x est uniformément continue, la démonstration est plus compliquée que pour la 1e fonction, car ici la dérivée n'est pas bornée. Par contre, on peut remarquer que sur l'intervalle 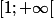, la dérivée est bornée, donc racine de x est unif. continue sur cet intervalle. Sur [0;2] elle est uniformément continue aussi car elle est continue et on est sur un segment. Pour tout 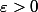, il existe r et r' > 0 tels que et .
Qu'est-ce qu'on pourrait choisir pour pour avoir ?

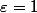g n'est pas uniformément continue sur ]0;1] (elle croît trop vite vers l'infini en 0), pour le prouver, on doit montrer que . On peut montrer qu' convient par exemple. Soit donc r > 0, on cherche x et y dans ]0,1] tels que et . Si on prend , avec n assez grand pour avoir , et ça doit marcher (il y a d'autres solutions possibles).