Construction d'un triangle!
17 messages
- Page 1 sur 1
Construction d'un triangle!
Sauriez-vous construire un triangle ABC, connaissant a, p, S, c'est-à-dire un côté, le demi-périmètre et la surface ???
Les trois coté du triangles sont trois vecteurs du plan repérés par leurs coordonnées (x,y).
Tu connais le premier vecteur.
Il faut donc déterminer les 4 coordonnées restantes.
Comme informations tu as: la somme des normes des vecteurs = périmètre
et 1/2*déterminant de 2 vecteurs du triangle = S.
Ca fais 4 équations, et 4 inconnues!
J'espère que je ne me suis pas trompé!
Tu connais le premier vecteur.
Il faut donc déterminer les 4 coordonnées restantes.
Comme informations tu as: la somme des normes des vecteurs = périmètre
et 1/2*déterminant de 2 vecteurs du triangle = S.
Ca fais 4 équations, et 4 inconnues!
J'espère que je ne me suis pas trompé!
Darko a écrit:Les trois coté du triangles sont trois vecteurs du plan repérés par leurs coordonnées (x,y).
Tu connais le premier vecteur.
Il faut donc déterminer les 4 coordonnées restantes.
Comme informations tu as: la somme des normes des vecteurs = périmètre
et 1/2*déterminant de 2 vecteurs du triangle = S.
Ca fais 4 équations, et 4 inconnues!
J'espère que je ne me suis pas trompé!
et moi, je me suis mal expliqué!
Il s'agit, bien sûr, de construire ce triangle (à un déplacement près) à la règle et au compas
ffpower a écrit:ben une fois que ta la longueur des cotés,c pas compliqué.
J'essaie de réexpliquer, puisque visiblement, çà a du mal. Je dispose de deux longueurs (a et p) et une surface (par exemple un carré de côté s).
Je ne fais aucun calcul. Je veux construire, à la règle et au compas, un rectangle, à un déplacement près, ayant ce côté, ce périmètre et cette surface.
Je ne comprends pas ce qui n'est pas compris.
Salut,
Bon, j'ai pas reussi a trouver mais je pense avoir une piste.
Je suppose qu'on a droit a la division...
Pour la surface:
On trace le segment de longueur connue (a).
Ensuite, on trace un segment perpendiculaire a ce segment passant par un de ses cotés, de longueur h, tel que ah=2S.
Apres on trace une parallele au premier segment passant par le bord de notre perpendiculaire (genre pour faire un rectangle).
Le dernier point se situe sur cette parallele Aire triangle=a*h/2=S
Pour le demi perimetre:
On trace la parallele a notre coté de longueur a et passant par le milieu de celui de longueur h.
On peut prendre le milieu du coté de longueur h, pareil pour celui de longueur a, et les joindre. On obtient un triangle semblable de rapport 1/2. La somme des cotés fera donc p.
Apres il faudrait a trouver le dernier point C, en le faisant 'coulisser' sur la parallele de telle que sorte que les distance tombent bien, mais je vois pas :hein:
En espérant etre utile... :marteau:
Bon, j'ai pas reussi a trouver mais je pense avoir une piste.
Je suppose qu'on a droit a la division...
Pour la surface:
On trace le segment de longueur connue (a).
Ensuite, on trace un segment perpendiculaire a ce segment passant par un de ses cotés, de longueur h, tel que ah=2S.
Apres on trace une parallele au premier segment passant par le bord de notre perpendiculaire (genre pour faire un rectangle).
Le dernier point se situe sur cette parallele Aire triangle=a*h/2=S
Pour le demi perimetre:
On trace la parallele a notre coté de longueur a et passant par le milieu de celui de longueur h.
On peut prendre le milieu du coté de longueur h, pareil pour celui de longueur a, et les joindre. On obtient un triangle semblable de rapport 1/2. La somme des cotés fera donc p.
Apres il faudrait a trouver le dernier point C, en le faisant 'coulisser' sur la parallele de telle que sorte que les distance tombent bien, mais je vois pas :hein:
En espérant etre utile... :marteau:
la vie est une fête 
Bonjour jver,
l'énoncé de ta question est incomplet. En effet, il est indispensable de préciser sous quelle forme l'aire S est donnée. Par exemple si l'on dit que l'aire S est celle d'un cercle donné, la construction est impossible à la règle et au compas. Elle est possible dans d'autres cas. La possibilité de construire dépend de la façon dont l'énoncé précise exactement comment l'aire S est donnée au départ.
Supposons que cette donnée soit bien précisée et que, par suite, l'on puisse construire un segment de longueur h=S/2a
Je ne peut pas décrire la construction de ce segment puisque je ne sais pas comment l'aire S est donnée. Supposons donc que le segment h soit construit (ce n'est pas la partie difficile du problème en général).
On va d'abord tracer une figure auxiliaire :
- Construire le triangle rectangle EFG (rectangle en G) dont l'hypoténuse EF est de longueur (2p-a) et dont le coté EG est de longueur a.
- Sur le coté GF, placer le point I tel que GI = h
- Tacer la droite parallèle à EF passant par I. Elle coupe la droite EG au point J.
- Tacer le cercle de centre J et de rayon = (a/2). Ce cercle coupe la droite GF en deux points. Désignons par K celui des deux qui se trouve du même coté que F par rapport à G (autrement dit, K est sur la demi-droite GF)
- Sur la demi-droite GF, traçons le point P tel que GP = p-(a/2)
Résultat : la longeur du segment KP est égale à la longueur (b) d'un des cotés du triangle ABC que l'on cherche à construire.
Figure principale, construction du triangle ABC :
- Tracer AB de longueur =a
- Tracer la droite (D) parralèle à AB avec la distance h entre elles.
- tracer le cercle de centre A et de rayon = KP (prouvé par la construction précédente. Ce cercle coupe (D) en deux points C1 et C2. Comparer avec (2p) les longueurs (AB+AC1+BC1) et (AB+AC2+BC2). Le point C est celui des deux qui donne l'égalité à (2p).
Remarque : si l'une des constructions indiquées s'avère impossible, c'est que les données (a, p, S) n'ont pas la cohérence requise pour qu'il existe un triangle ABC répondant aux conditions imposées.
l'énoncé de ta question est incomplet. En effet, il est indispensable de préciser sous quelle forme l'aire S est donnée. Par exemple si l'on dit que l'aire S est celle d'un cercle donné, la construction est impossible à la règle et au compas. Elle est possible dans d'autres cas. La possibilité de construire dépend de la façon dont l'énoncé précise exactement comment l'aire S est donnée au départ.
Supposons que cette donnée soit bien précisée et que, par suite, l'on puisse construire un segment de longueur h=S/2a
Je ne peut pas décrire la construction de ce segment puisque je ne sais pas comment l'aire S est donnée. Supposons donc que le segment h soit construit (ce n'est pas la partie difficile du problème en général).
On va d'abord tracer une figure auxiliaire :
- Construire le triangle rectangle EFG (rectangle en G) dont l'hypoténuse EF est de longueur (2p-a) et dont le coté EG est de longueur a.
- Sur le coté GF, placer le point I tel que GI = h
- Tacer la droite parallèle à EF passant par I. Elle coupe la droite EG au point J.
- Tacer le cercle de centre J et de rayon = (a/2). Ce cercle coupe la droite GF en deux points. Désignons par K celui des deux qui se trouve du même coté que F par rapport à G (autrement dit, K est sur la demi-droite GF)
- Sur la demi-droite GF, traçons le point P tel que GP = p-(a/2)
Résultat : la longeur du segment KP est égale à la longueur (b) d'un des cotés du triangle ABC que l'on cherche à construire.
Figure principale, construction du triangle ABC :
- Tracer AB de longueur =a
- Tracer la droite (D) parralèle à AB avec la distance h entre elles.
- tracer le cercle de centre A et de rayon = KP (prouvé par la construction précédente. Ce cercle coupe (D) en deux points C1 et C2. Comparer avec (2p) les longueurs (AB+AC1+BC1) et (AB+AC2+BC2). Le point C est celui des deux qui donne l'égalité à (2p).
Remarque : si l'une des constructions indiquées s'avère impossible, c'est que les données (a, p, S) n'ont pas la cohérence requise pour qu'il existe un triangle ABC répondant aux conditions imposées.
fatal_error a écrit:Salut,
Bon, j'ai pas reussi a trouver mais je pense avoir une piste.
Je suppose qu'on a droit a la division...
Pour la surface:
On trace le segment de longueur connue (a).
Ensuite, on trace un segment perpendiculaire a ce segment passant par un de ses cotés, de longueur h, tel que ah=2S.
Apres on trace une parallele au premier segment passant par le bord de notre perpendiculaire (genre pour faire un rectangle).
Le dernier point se situe sur cette parallele Aire triangle=a*h/2=S
Pour le demi perimetre:
On trace la parallele a notre coté de longueur a et passant par le milieu de celui de longueur h.
On peut prendre le milieu du coté de longueur h, pareil pour celui de longueur a, et les joindre. On obtient un triangle semblable de rapport 1/2. La somme des cotés fera donc p.
Apres il faudrait a trouver le dernier point C, en le faisant 'coulisser' sur la parallele de telle que sorte que les distance tombent bien, mais je vois pas :hein:
En espérant etre utile... :marteau:
Vous êtes sur la bonne piste! mais ce n'est pas fini.
En effet, on commence par construire la longueur a
Ensuite,on utilise S=pr =s^2 pour construire r (triangle rectangle de hauteur s et d'hypothénuse p+r ...)
Une fois cela obtenu, on porte sur une perpendiculaire à BC les longeurs h,r et on construit donc le point tel que ces quatre points forment une division harmonique. Cela donne la valeur de ra, rayon du cercle exinscrit dans l'angle A
On n'a pas encore fini; en effet il existe une propriété miraculeuse du cercle circonscrit qui coupe la médiatrice de BC en un point K tel que KA'=(ra-r)/2 (A' est le milieu de BC) --pas difficile à montrer. Comme on a r et ra, on peut donc construire le point K
On trace alors le cercle circonscrit à BCK, qui coupe la droite distante de h de BC en le point A (Il y en a deux, ou 0)
et c'est fini!
Maintenant,une autre manière, que j'aime moins: une fois qu'on a a, on a (b+c) puisque b+c=2p-a. Il suffit alors de faire l'intersection de l'ellipse de foyers B et C des points dont la somme des distances aux foyers esr b+c, avec la droite située à h de BC.
Si ce genre de problèmes intéresse, j'en ai une palanquée, dont certains faciles, d'autres difficiles, d'autres, enfin, que je n'ai pas résolu.
Salut
JJa a écrit:Bonjour jver,
l'énoncé de ta question est incomplet. En effet, il est indispensable de préciser sous quelle forme l'aire S est donnée. Par exemple si l'on dit que l'aire S est celle d'un cercle donné, la construction est impossible à la règle et au compas. Elle est possible dans d'autres cas. La possibilité de construire dépend de la façon dont l'énoncé précise exactement comment l'aire S est donnée au départ.
Supposons que cette donnée soit bien précisée et que, par suite, l'on puisse construire un segment de longueur h=S/2a
Je ne peut pas décrire la construction de ce segment puisque je ne sais pas comment l'aire S est donnée. Supposons donc que le segment h soit construit (ce n'est pas la partie difficile du problème en général).
On va d'abord tracer une figure auxiliaire :
- Construire le triangle rectangle EFG (rectangle en G) dont l'hypoténuse EF est de longueur (2p-a) et dont le coté EG est de longueur a.
- Sur le coté GF, placer le point I tel que GI = h
- Tacer la droite parallèle à EF passant par I. Elle coupe la droite EG au point J.
- Tacer le cercle de centre J et de rayon = (a/2). Ce cercle coupe la droite GF en deux points. Désignons par K celui des deux qui se trouve du même coté que F par rapport à G (autrement dit, K est sur la demi-droite GF)
- Sur la demi-droite GF, traçons le point P tel que GP = p-(a/2)
Résultat : la longeur du segment KP est égale à la longueur (b) d'un des cotés du triangle ABC que l'on cherche à construire.
Figure principale, construction du triangle ABC :
- Tracer AB de longueur =a
- Tracer la droite (D) parralèle à AB avec la distance h entre elles.
- tracer le cercle de centre A et de rayon = KP (prouvé par la construction précédente. Ce cercle coupe (D) en deux points C1 et C2. Comparer avec (2p) les longueurs (AB+AC1+BC1) et (AB+AC2+BC2). Le point C est celui des deux qui donne l'égalité à (2p).
Remarque : si l'une des constructions indiquées s'avère impossible, c'est que les données (a, p, S) n'ont pas la cohérence requise pour qu'il existe un triangle ABC répondant aux conditions imposées.
Vous avez bien entendu raison sur la manière de se donner S. J'avais oublié de le dire; dans ce genre de problème, on se donne s, côté du carré d'aire S (il apparaît, il me semble, dans la solution, d'autant plus qu'on a besoin de s sqrt(2) et que le carré est bien pratique pour cela!
Ceci dit, j'ai mis à midi une solution. Il peut y en avoir plusieurs et j'ai regardé avec attention la vôtre. Et je ne comprends pas pourquoi KP=b (ou c).
Si je ne me trompe pas:
- dans le triangle EFG rectangle, j'ai GE=a, EF (hypothénuse) = 2p-a et on a donc GF^2=4p(p-a)
- GJ/GI=GE/GF; GI=h et
GJ^2= h^2 a^2/(4p(p-a))
- On a GK^2=KJ^2-GJ^2= a^2/4-(ah)^2/(4p(p-a))= a^2/4(1-h^2/(p(p-a)))
Je ne comprends pas pourquoi la différence de cette grandeur (en prenant la racine carré) avec p-a/2 serait égal à b. J'essaie de "touiller" sans succès et, en fait, je ne comprends pas le fil directeur de la solution.
J'ajoute que, sur la figure que j'ai réalisée avec ma démonstration, je trouve que la solution convient (je trouve, il me semble, qu'elle est unique, à une symétrie près); je trouve enfin que, avec mes données, b=2,79 cm; avec votre construction, je trouve b= 2,77.
Donc, ... Je ne sais comment vous montrez cela?
Oui , bien sûr, il y a souvent différentes méthodes pour ce genre de constructions géométriques.
Celle que j'ai indiquée est la traduction géométrique de la relation analytique :
(p-(a/2)-b)² = (a/2)² - a²h²/(4p(p-a))
On voit que tous les paramètres sont connus, sauf b dans le membre de gauche. Cela permet de construire b.
Dans le triangle EFG, on trouve GF²=(2p-a)²-a²=4p(p-a)
Puis dans le triangle semblable JIG on trouve GI²=a²h²/(4p(p-a))
Dans le triangle JGK on trouve GK²=(a/2)² - a²h²/(4p(p-a))
Donc GK=p-(a/2)-b
Et avec GP=p-(a/2) on a la différence : KP=b.
Note : La relation analytique utilisée s'établit aisément par la méthode suivante :
Dans un triangle ABC avec AB=a, AC=b et BC=c, La projection orthogonale de C sur AB étant H, en posant AH=x et BH=y, on a le système d'équations :
2p=a+b+c
x+y=a
h²=b²-x²
h²=c²-y².
On élimine les paramètres x, y et c de ces équations, ce qui donne la relation analytique.
Celle que j'ai indiquée est la traduction géométrique de la relation analytique :
(p-(a/2)-b)² = (a/2)² - a²h²/(4p(p-a))
On voit que tous les paramètres sont connus, sauf b dans le membre de gauche. Cela permet de construire b.
Dans le triangle EFG, on trouve GF²=(2p-a)²-a²=4p(p-a)
Puis dans le triangle semblable JIG on trouve GI²=a²h²/(4p(p-a))
Dans le triangle JGK on trouve GK²=(a/2)² - a²h²/(4p(p-a))
Donc GK=p-(a/2)-b
Et avec GP=p-(a/2) on a la différence : KP=b.
Note : La relation analytique utilisée s'établit aisément par la méthode suivante :
Dans un triangle ABC avec AB=a, AC=b et BC=c, La projection orthogonale de C sur AB étant H, en posant AH=x et BH=y, on a le système d'équations :
2p=a+b+c
x+y=a
h²=b²-x²
h²=c²-y².
On élimine les paramètres x, y et c de ces équations, ce qui donne la relation analytique.
emdro a écrit:Bonsoir,
Je n'ai pas tout lu, mais d'après la formule de Héron,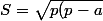(p-b)(p-c)})
Et donc, en l'adaptant à votre problème:
D'où
Or.
Cela peut être une piste, non?
J'avais pensé à cela, également; mais je ne trouve pas que cela donne quelque chose. Je continue à ne pas comprendre ... ce qui ne prouve pas grand-chose!
JJa a écrit:Oui , bien sûr, il y a souvent différentes méthodes pour ce genre de constructions géométriques.
Celle que j'ai indiquée est la traduction géométrique de la relation analytique :
(p-(a/2)-b)² = (a/2)² - a²h²/(4p(p-a))
On voit que tous les paramètres sont connus, sauf b dans le membre de gauche. Cela permet de construire b.
Dans le triangle EFG, on trouve GF²=(2p-a)²-a²=4p(p-a)
Puis dans le triangle semblable JIG on trouve GI²=a²h²/(4p(p-a))
Dans le triangle JGK on trouve GK²=(a/2)² - a²h²/(4p(p-a))
Donc GK=p-(a/2)-b
Et avec GP=p-(a/2) on a la différence : KP=b.
Note : La relation analytique utilisée s'établit aisément par la méthode suivante :
Dans un triangle ABC avec AB=a, AC=b et BC=c, La projection orthogonale de C sur AB étant H, en posant AH=x et BH=y, on a le système d'équations :
2p=a+b+c
x+y=a
h²=b²-x²
h²=c²-y².
On élimine les paramètres x, y et c de ces équations, ce qui donne la relation analytique.
Bon, je regarderai mieux demain. Là, je ne vois pas bien!
Mais, avec mes plus plates excuses, "ma" solution, est entièrement géométrique, et ne fait apparaître aucun calcul; juste un théorème qui dit que A'K=(ra-r)/2.
J'ai donc la faiblesse de préférer ma solution; ce qui me turlupine plus encore, c'est que "ma" solution répond à la question posée; je ne pense pas que la vôtre y réponde! Pouvons-nous échanger des figures?
Bonne nuit!
Il ne faut pas tout confondre !
- Une chose est la construction à la règle et au compas dont on donne toutes les étapes permettant de la réaliser.
- Une autre chose est la preuve que la construction est exacte. Cette preuve peut être faitre par n'importe quelle méthode, géométrique ou analytique, avec des formules ou sans formule, en faisant appel à des théorèmes connus, etc., peu importe : cela ne fait pas partie de ce qu'on appelle "la construction à la règle et au compas". Ce n'est pas avec la règle et le compas que l'on fait et que l'on rédige la démonstration !
Résumons nous :
- Un problème de construction à la règle et au compas a été posé.
- Une réponse a été donnée dans le post #7 du 13/04 à 12h03. Elle satisfait plainement à la question posée.
- Peut importe la façon dont la preuve d'exactitude a été expliquée ultérieurement : il y a toujours plusieurs méthodes possibles pour les démonstrations. Cela n'a rien à voir avec l'intérêt, ou non, de la construction à la règle et au compas.
Personnellement, je n'ai aucune préférence pour cette construction ou pour une autre. Il y a probablement d'autres constructions plus simples : Généralement on trouve plus simple en cherchant plus.
La préférence d'une construction par rapport à une autre est une question personnelle, selon des critères qui ne sont pas les mêmes selon les personnes. Donc, je ne milite pas pour que cette construction soit préférée à une autre : c'est indiférent.
- Une chose est la construction à la règle et au compas dont on donne toutes les étapes permettant de la réaliser.
- Une autre chose est la preuve que la construction est exacte. Cette preuve peut être faitre par n'importe quelle méthode, géométrique ou analytique, avec des formules ou sans formule, en faisant appel à des théorèmes connus, etc., peu importe : cela ne fait pas partie de ce qu'on appelle "la construction à la règle et au compas". Ce n'est pas avec la règle et le compas que l'on fait et que l'on rédige la démonstration !
Résumons nous :
- Un problème de construction à la règle et au compas a été posé.
- Une réponse a été donnée dans le post #7 du 13/04 à 12h03. Elle satisfait plainement à la question posée.
- Peut importe la façon dont la preuve d'exactitude a été expliquée ultérieurement : il y a toujours plusieurs méthodes possibles pour les démonstrations. Cela n'a rien à voir avec l'intérêt, ou non, de la construction à la règle et au compas.
Personnellement, je n'ai aucune préférence pour cette construction ou pour une autre. Il y a probablement d'autres constructions plus simples : Généralement on trouve plus simple en cherchant plus.
La préférence d'une construction par rapport à une autre est une question personnelle, selon des critères qui ne sont pas les mêmes selon les personnes. Donc, je ne milite pas pour que cette construction soit préférée à une autre : c'est indiférent.
JJa a écrit:Il ne faut pas tout confondre !
- Une chose est la construction à la règle et au compas dont on donne toutes les étapes permettant de la réaliser.
- Une autre chose est la preuve que la construction est exacte. Cette preuve peut être faitre par n'importe quelle méthode, géométrique ou analytique, avec des formules ou sans formule, en faisant appel à des théorèmes connus, etc., peu importe : cela ne fait pas partie de ce qu'on appelle "la construction à la règle et au compas". Ce n'est pas avec la règle et le compas que l'on fait et que l'on rédige la démonstration !
Résumons nous :
- Un problème de construction à la règle et au compas a été posé.
- Une réponse a été donnée dans le post #7 du 13/04 à 12h03. Elle satisfait plainement à la question posée.
- Peut importe la façon dont la preuve d'exactitude a été expliquée ultérieurement : il y a toujours plusieurs méthodes possibles pour les démonstrations. Cela n'a rien à voir avec l'intérêt, ou non, de la construction à la règle et au compas.
Personnellement, je n'ai aucune préférence pour cette construction ou pour une autre. Il y a probablement d'autres constructions plus simples : Généralement on trouve plus simple en cherchant plus.
La préférence d'une construction par rapport à une autre est une question personnelle, selon des critères qui ne sont pas les mêmes selon les personnes. Donc, je ne milite pas pour que cette construction soit préférée à une autre : c'est indiférent.
Peut-être que je confond tout.
Mais je trouve intéressant que, sur un problème aussi "simple", on puisse faire affronter des visions aussi différentes!;
Votre première remarque sur la manière dont est définie la surface S est pertinente.
Ensuite, votre construction est fondée sur la transcription géométrique d'un ensemble d'équations. J'ai refait, avec attention, votre solution, et elle aboutit au même triangle que la mienne. En ce sens, elle est exacte comme la mienne l'est (moi, j'ai regardé la vôtre, avez-vous regardé la mienne?).
Pour moi -- je ne suis pas seul! -- la construction "à la règle et au compas" est une suite de "gestes" dont chacun puise sa pertinence sur une propriété géométrique. Sinon, à mon sens, on perd toute l' "esthétique" de la construction. Et je n'aime pas les mathématiques privées de leur esthétique!
Je ne sais pas si j'exprime bien, mais je ne peux que réagir quand vous dites que "Une chose est la construction à la règle et au compas... Une autre chose est la preuve que la construction est exacte." C'est cette dichotomie entre la construction et la preuve que je trouve choquante. Enfin, qui me choque.
Ceci dit, je ne suis pas accroché à la solution que j'ai présentée; je serais ravi que quelqu'un en trouve une plus "jolie", plus compacte, plus élégante. Mais ces "valeurs" existent-elles?
Bonne après-midi.
17 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 47 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
