Une petite curiosité même si je n'ai pas le sujet entier. 1968 est, je crois, la première année où les lauréats ont été reçus à l'Elysée et non pas à la Sorbonne (lieu dangereux

)
La notation

désigne la fonction partie entière sur

.
1) Un couple
)
de réels étant donné, encadrer les entier relatifs E(x+y) et E(y).
2) L'entier relatif a étant donné, définir l'ensemble des couples (x,u) de réels vérifiant
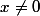
et l'égalité
=a)
. Le représenter graphiquement suivant les divers cas qui peuvent se produire.
3) L'entier relatif a étant donné, définir l'ensemble des couples (x,u) de réels vérifiants

et l'égalité
}{x}})=a)
. Le représenter graphiquement suivant les divers cas qui peuvent se produire.
Préciser en particulier l'ensemble
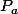
des valeurs de cx pour lesquelles l'ensemble correspondant des couples (x,u) n'est pas vide, en distinguant notamment les cas
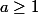

,
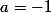
et

4) Pour tout couple (x,y) de réels vérifiant

et tout entier relatif a, on pose
=E(\displaystyle{\frac{E(xy)}{x}}))
et l'on note
)
l'ensemble des réels y tels que f(x,y)=a.
a)Montrer que
)
admet, s'il n'est pas vide, un minimum noté
)
. Admet-il un maximum ?
b) Etudiez l'application
)
, c'est-à-dire notamment déterminer les couples (a,x) pour lesquels
)
est définie, et la représenter graphiquement pour

.
c) Comparer
)
là où cela a un sens. On commencera par examiner le cas où x est entier. S'il ne l'est pas et vérifie x>1, on cherchera dans

un y tel que xy ne soit pas dans

et l'on déterminera un encadrement simple de la forme
\leq f(x,y)\leq\beta(x))
.
6) Et si x<0 ? (reprendre les questions 3 à 5)
D'après CG 1968
A vos crayons (pour les courageux, un peu sec comme sujet)
