Composition de developpements limités

[gfalkio]

Bonjour,

Je suis entrain de voir les développements limités. Pour les calculs de fonctions usuelles (exp, sin, cos...) je parviens à les faire.

Cependant je ne vois pas complètement comment faire pour la composition de développements limités. Je ne sais pas ce que j'ai le droit de faire ? comment le faire, quelles étapes.. etc

Exemple

au point 0, d'ordre disons 4, peu importe c'est la méthode qu'il me manque.

Comment commencer ? développer sin(x) ? et ensuite ?

Quelles sont les règles à respecter ?

Merci !

[arnaud32]

peux tu donner un dl de \sqrt{1+u} au voisinage de 0? et sin(x) au voisinage de 0?

[gfalkio]

Pour ce genre de développement limités ca va,, c'est surtout la composition, je vois pas comment faire vraiment, qu'estce que j'a ile droit de faire/pas faire, contraintes à respecter ? conditions necessaires pour pouvoir le faire ... ?
merci de ta réponse.

[Mathusalem]

.

Ton développement de n'est pas tout à fait correct.

[gfalkio]

oups innatention il manque le terme en et la factorielle, ce qui donne
:

[Mathusalem]

oups innatention il manque le terme en et la factorielle, ce qui donne
:

Toujours pas. De plus, si 'u' est ta variable, tu devrais avoir un développement en u, pas en x.

La faute que tu fais est le calcul de f(0)

[gfalkio]

Ah oui en effet je devrais avoir u et non x.
De plus tu as encore raison, en 0 est égal à 1.

Je pense qu'il est correct maintenant ?

[Mathusalem]

oui il l'est.

[gfalkio]

Ok donc revenons au problème principal, la composition de dl ?

[Mathusalem]

Tu as la fonction



Dont tu cherches le DL autour de la variable x = 0.

Pourquoi est-ce que l'on t'a demandé de faire le developpement de sin(x) autour de x = 0, et de sqrt(1+u) autour de u = 0 ?

[gfalkio]

Peit-être parce que je vais devoir remplacer les u par le dl de sin(x) dans mon dl de ? mais qu'estce que je fais du premier terme ? et si a la place de sin(x) j'aurai eu une autre fonction dont le dl aurait eu un premier terme constant différent de 0 ? quels sont les règles à suivre ?

[Mathusalem]

Dans la suite je développe au 2è voire 3è ordre les termes séparements. Je vais pas écrire les O(...)


autour de x = 0
autour de u = 0


Donc, autour de x = 0,

On prend maintenant autour de x = 0.
autour de x = 0

autour de u = 1.

Donc autour de x = 1

Mais pourquoi autour de u = 1 ? Parce que si je développe autour de x = 0, la valeur du cosinus bouge autour de 1. Donc je suis obligé de développer ma fonction autour de 1, comme si cos(x) était sa variable.

Si on avait demandé le DL de autour de x = pi/4, alors on devrait développer autour de

EDIT: Mais tout cela, ce n'est que pour te faciliter la vie hein !
Tu peux très bien faire le développement limité brutal de autour de x = 0. Sauf que les dérivées successives de f(x) sont très chiantes à calculer. C'est pour ça que tu passes par la composition de DL

[gfalkio]

Ok pour le premier, mais après je comprend pas pourquoi tu changes de point, et comment tu trouves le trouves le nouveau point !

Ensuite j'ai d'autres questions mais cette fois ci concernant les limites avec le développement limité.

Comment faire les limites avec des développements limités ? exemple
lim en x =0 de

Je sais que la réponse est -1/120, j'a suivi un peu le corrigé mais je comprend pas certains éléments.

ILe corrigé dit que , déjà pourquoi o(x^5) ? le terme en x^5 est déjà développé !
Ensuite il factorise la lim qu'on cherche par 1/x^5 et puis surgit lim x en 0 = = -1/120 ! presque totalement incompréhensible.

[Mathusalem]

Ok pour le premier, mais après je comprend pas pourquoi tu changes de point, et comment tu trouves le trouves le nouveau point !

Alors :

Calcule le développement limité de :

autour de 0.

Qu'est-ce que tu fais ? Tu dérives brutalement cette fonction ? Ou est-ce que tu vas pas à pas ?

On commence au niveau le plus profond : 1 + e^(x).

1. Il faut développer autour de 0 e^(x)



2. On prend le niveau supérieur, c'est la fonction
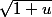
Mais u, c'est e^x. et x varie autour de 0. Or, si x varie autour de 0, e^x varie autour de 1 (e^0 = 1). Donc u varie autour de 1.

Ainsi, tu dois développer autour de u = 1.

et tu obtiens



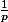
Ensuite, le niveau suivant, c'est la fonction (la puissance -1).

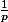
Mais, quand x varie autour de 0, e^x varie autour de 1, et varie autour de . Donc tu devras développer autour de p =

et donc



Ensuite le dernier niveau c'est la fonction tan(y). Mais lorsque x varie autour de 0, e^x varie autour de 1, sqrt(1+e^x) varie autour de sqrt(2), et sqrt(1+e^x)^-1 varie autour de 1/sqrt(2)

Donc tu vas développer tan(y) autour de y = 1/sqrt(2)



Et quand tu remets tout ensemble, tu obtiens alors un truc trop dégueulasse pour le récrire ici.

Pour ce qui est de la limite,

développe le sinus plus loin que l'ordre 5, mettons l'ordre 9.

Tu vas te retrouver avec l'expression Autrement dit, tu peux récrire ça comme

Les grands termes tendent à 0 en x = 0.

[gfalkio]

Merci pour ta réponse, je vois beuaocup mieux le cheminement !

Pour vérifier si j'ai bien compris j'ai essayé un autre exemple :



J'ai donc développé cos(x) en 0 comme demandé dans l'énoncé:

Puis ln(u), si je résonne bien, u c'est cos(x) et x varie autour de 0, donc cos(x) varie autour de 1. J dois donc développer autours de 1 :



Je reste l'ordre 2 pour simplifier l'écriture sur le forum :

ainsi ln(cos(x)) =
ce qui donne
:
Le résultat obtenu par le prof n'est pas loin mais pas le meme, il part du fait que cos (x) = 1 + X ( en développant) et qu'on connait le dl de ln(1+x), le calcul devient plus formel, lui cependant restreint x de -pi/2 a pi/22, hmm pourquoi ?

et puis dans l'énoncé c'est demandé développer autour de 0 ! estce que je respecte tout de même la consigne si je fais comme plus haut ?

Merci !

[Mathusalem]

Merci pour ta réponse, je vois beuaocup mieux le cheminement !

Pour vérifier si j'ai bien compris j'ai essayé un autre exemple :



J'ai donc développé cos(x) en 0 comme demandé dans l'énoncé:

Puis ln(u), si je résonne bien, u c'est cos(x) et x varie autour de 0, donc cos(x) varie autour de 1. J dois donc développer autours de 1 :

Jusque là, c'est bon.
Tu dois développer ln(u) autour de u = 1. Et toi pour le faire, tu l'as dérivé selon x. Non !

autour de u = 1
autour de u = 1.
car la première dérivée est 1/u et la deuxième -1/u^2

La formule que tu obtiens pour le développement de ln(u) c'est enfait le DL de (ln(u(x)) autour de x = 0.
Je te rappelle de plus que tu ne peux pas avoir des termes en x si ta variable est u dans un développement.

Tu dois réfléchir vraiment en termes séparés : soit tu vas brutal et tu dévelopes g(x) = ln(cos(x)) au deuxième ordre autour de x = 0 avec
g'(x) = -tan(x)
g''(x) = -sec^2(x)

Et donc

Soit tu décomposes le DL
autour de x = 0
autour de u = 1
Et tu introduis

Pour retrouver

(remarque sec^2(0) = 1)

Ton prof s'est gourré si c'est ça son corrigé parce que 1 + X c'est pas le DL de cos autour de 0.

Pour ce qu'il en est de la restriction, regarde ce qu'il se passe quand x prend les valeurs -pi/2 et pi/2.

[gfalkio]

Ah ! Je comprend de mieux en mieux ! a force de faire des dl autours de 0, j'en oublie presque que que c'est
(x-a)^n et non x uniquement parce que a = 0
Pour ce qui est du corrigé quand il dit 1+X il sous entend que X = le dl de cos(x) sans le terme constant autours de 0.

Pour ce qui est des limites je pense avoir compris.

Pour la restriction de -pi/2 pi/2, c'est parce que cos(pi/2) c'est 0 et que ln(0) n'existe pas, je pense ?

Il faut donc que je fasse attention lors de mes développements limités, quelle est la variable avec laquelle je développe, du point autours duquel je travaille.

Merci beaucoup mathusalem !

J'ai encore une question, cette fois ci il s'agit des notations o(x) et O(x).
Quand les écrire ? a chaque dl que je fais ? meme s'il s'agit d'un intermediaire par exemple ln(u) ?

estce que je peux dire que cos(x) = pour pouvoir faire un produit ou quotient avec sin(x) = meme si le dernier terme développé de cos(x) c'est du x^2 ?