Comparaison de deux suites
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Sylvain200
- Membre Naturel
- Messages: 25
- Enregistré le: 13 Déc 2016, 17:09
-
 par Sylvain200 » 10 Déc 2021, 21:22
par Sylvain200 » 10 Déc 2021, 21:22
Bonsoir,
J'ai les suites suivantes définies par:
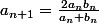
et
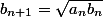
.
Supposons que
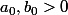
. A-t-on
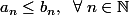
?
Cordialement,
Sylvain.
-
lyceen95
- Membre Complexe
- Messages: 2263
- Enregistré le: 14 Juin 2019, 23:42
-
 par lyceen95 » 10 Déc 2021, 22:25
par lyceen95 » 10 Déc 2021, 22:25
Si
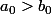
, ça s'engage mal.
Reste à regarder ce qui se passe quand
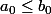
-
Sylvain200
- Membre Naturel
- Messages: 25
- Enregistré le: 13 Déc 2016, 17:09
-
 par Sylvain200 » 11 Déc 2021, 07:26
par Sylvain200 » 11 Déc 2021, 07:26
D'accord. On peut montrer que

.
De cette inégalité, on peut montrer aussi que :
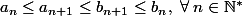
Est-ce-qu'on peut déduire que les suites
)
et
)
sont convergentes?
L’inégalité ci-dessus donne que , par exemple,
)
est croissante (si
)
et majorée .
Bien sûr si
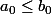
, aucun probléme, puisque l'inégalité ci-dessus sera vraie pour tout
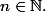
Mais si on a
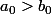
, est ce que ça va influer sur la convergence des suites?
-
lyceen95
- Membre Complexe
- Messages: 2263
- Enregistré le: 14 Juin 2019, 23:42
-
 par lyceen95 » 11 Déc 2021, 08:57
par lyceen95 » 11 Déc 2021, 08:57
La formule est symétrique : dans le calcul de

, les nombres

et

jouent le même rôle.
Et pareil dans la formule de
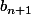
Donc, si on commence par exemple par
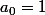
et
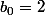
, ou bien par
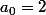
et
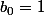
, le premier terme est différent, mais tous les autres termes des 2 suites sont strictement les mêmes.
Dès que n>0,
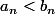
Est-ce qu'on peut en déduire que les suites
)
et
)
sont convergentes ?
Non, ça ne suffit pas.
Imagine les suites :
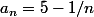
et
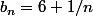
Elles vérifient bien la série d'inégalités que tu donnes, mais...
-
catamat
- Habitué(e)
- Messages: 1365
- Enregistré le: 07 Mar 2021, 10:40
-
 par catamat » 11 Déc 2021, 10:31
par catamat » 11 Déc 2021, 10:31
Sylvain200 a écrit:on peut montrer aussi que :
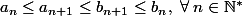
Est-ce-qu'on peut déduire que les suites
)
et
)
sont convergentes?
Bonjour
La suite
)
est croissante et majorée par
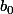
donc elle est convergente
De même
)
est décroissante et minorée par

donc elle est convergente
Par contre elles s'ont pas nécessairement la même limite comme dans l'exemple de Lycéen95.
-
Sylvain200
- Membre Naturel
- Messages: 25
- Enregistré le: 13 Déc 2016, 17:09
-
 par Sylvain200 » 11 Déc 2021, 10:55
par Sylvain200 » 11 Déc 2021, 10:55
J'ai pas bien saisi vos réponses. A-t-on la convergence des suites peu n'importe
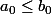
ou
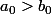
?
@catamat, je ne suis pas d'accord avec vous, si on a la convergence, alors on a l'égalité de deux limites.
-
catamat
- Habitué(e)
- Messages: 1365
- Enregistré le: 07 Mar 2021, 10:40
-
 par catamat » 11 Déc 2021, 11:43
par catamat » 11 Déc 2021, 11:43
Voir l'exemple donné par Lycéen95 l'une croissante a pour limite 5 l'autre décroissante a pour limite 6
-
Sylvain200
- Membre Naturel
- Messages: 25
- Enregistré le: 13 Déc 2016, 17:09
-
 par Sylvain200 » 11 Déc 2021, 12:01
par Sylvain200 » 11 Déc 2021, 12:01
Pour les suites que j'ai donné, ce n'est pas le cas.
Si elles convergent, nécessairement elles ont la
même limite.
-
mathelot
 par mathelot » 11 Déc 2021, 13:04
par mathelot » 11 Déc 2021, 13:04
Sylvain200 a écrit:Pour les suites que j'ai données, ce n'est pas le cas.
Si elles convergent, nécessairement elles ont la
même limite.
oui,les deux suites sont adjacentes. Les limites l de an et l' de bn vérifient l'égalité l(l-l')=0
l étant non nulle,l=l'
Modifié en dernier par mathelot le 11 Déc 2021, 17:32, modifié 1 fois.
-
lyceen95
- Membre Complexe
- Messages: 2263
- Enregistré le: 14 Juin 2019, 23:42
-
 par lyceen95 » 11 Déc 2021, 13:17
par lyceen95 » 11 Déc 2021, 13:17
Il y a eu un quiproquo.
Dire que 2 suites sont convergentes, ça ne veut pas forcément dire qu'elles ont la même limite. Suites convergentes, ou suites adjacentes, ce n'est pas pareil.
Donc mon contre-exemple était hors-sujet.
Ici, tu affirmes que ces 2 suites ont la même limite. Ok. Mais affirmer quelque chose, ça ne sert à rien. Il faut le prouver.
-
mathelot
 par mathelot » 11 Déc 2021, 13:36
par mathelot » 11 Déc 2021, 13:36
Sylvain200 a écrit: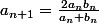
Soit l la limite de (a_n) et l' la limite de (b_n)
On passe à la limite dans l'égalité,il vient:
l=2ll'/(l+l')
Soit
l^2+ll'=2ll'
l(l-l')=0
l=l' car l>0
Modifié en dernier par mathelot le 13 Déc 2021, 22:05, modifié 3 fois.
-
Sylvain200
- Membre Naturel
- Messages: 25
- Enregistré le: 13 Déc 2016, 17:09
-
 par Sylvain200 » 11 Déc 2021, 13:38
par Sylvain200 » 11 Déc 2021, 13:38
On a
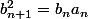
, donc
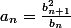
et par suite si les deux suites convergent, elles ont la même limite.
-
Sylvain200
- Membre Naturel
- Messages: 25
- Enregistré le: 13 Déc 2016, 17:09
-
 par Sylvain200 » 11 Déc 2021, 13:42
par Sylvain200 » 11 Déc 2021, 13:42
Ma question est la suivante: les suites (a_n) et (b_n) sont-elles convergentes? peu n'importe
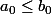
ou
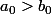
ou faut-il imposer la condition
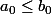
pour assurer la convergence?
-
catamat
- Habitué(e)
- Messages: 1365
- Enregistré le: 07 Mar 2021, 10:40
-
 par catamat » 11 Déc 2021, 15:18
par catamat » 11 Déc 2021, 15:18
On t'a déjà répondu à cette question :
lyceen95 a écrit:La formule est symétrique : dans le calcul de

, les nombres

et

jouent le même rôle.
Et pareil dans la formule de
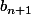
Donc, si on commence par exemple par
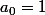
et
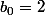
, ou bien par
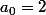
et
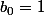
, le premier terme est différent, mais tous les autres termes des 2 suites sont strictement les mêmes.
-
mathelot
 par mathelot » 11 Déc 2021, 17:24
par mathelot » 11 Déc 2021, 17:24
La limite commune des deux suites est strictement positive car la suite an est croissante à partir du rang 1 et son terme a1 est strictement positif.
Modifié en dernier par mathelot le 15 Déc 2021, 14:38, modifié 1 fois.
-
Sylvain200
- Membre Naturel
- Messages: 25
- Enregistré le: 13 Déc 2016, 17:09
-
 par Sylvain200 » 11 Déc 2021, 17:44
par Sylvain200 » 11 Déc 2021, 17:44
J'ai pas bien saisi l'argument utilisé.
Si a_0 >b_0, quel est l'argument utilisé pour montrer la convergence des suites ? car dans ce cas, je pense que la suite, par exemple,( a_n) n'est pas croissante.
Me trompe-je ?
-
mathelot
 par mathelot » 13 Déc 2021, 21:36
par mathelot » 13 Déc 2021, 21:36
pour
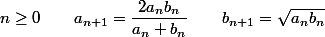
i)
suites strictement positives 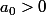
et
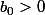
Par récurrence immédiate : pour

et
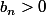
ii)
comparaison des suites:^2}{a_n+b_n} \geq 0)
pour
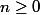
Pour
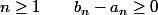
iii)
(a_n) croissantepour
}{a_n+b_n} \geq 0)
pour

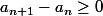
pour

iv)
suite (b_n) décroissante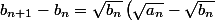 \leq 0)
pour

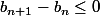
pour

v)

preuve:
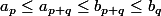
vi)
suites convergentesla suite (a_n) est croissante, majorée, à valeurs réelles.Elle converge vers une limite notée l.
la suite (b_n) est décroissante, minorée, à valeurs réelles.Elle converge vers une limite notée l'.
vii)
Egalité des limites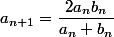
en passant à la limite , quand n tend vers

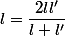
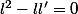
=0)
comme
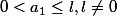
d'où
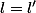
Les deux suites sont adjacentes.
remarque:
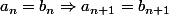
-
Sylvain200
- Membre Naturel
- Messages: 25
- Enregistré le: 13 Déc 2016, 17:09
-
 par Sylvain200 » 17 Déc 2021, 19:22
par Sylvain200 » 17 Déc 2021, 19:22
@mathelot, merci beaucoup pour votre réponse.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 44 invités
et
sont convergentes?
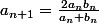
, les nombres
et
jouent le même rôle.
et
, ou bien par
et
, le premier terme est différent, mais tous les autres termes des 2 suites sont strictement les mêmes.