Bonjour,
Les réunions finies de segments sont des compacts de IR.
Y'a-t-il d'autres compacts de IR?
Compacts de IR
5 messages
- Page 1 sur 1
Re: compacts de IR
Bonjour,
Dans la topologie usuelle, tous les fermés bornés. Ainsi l'ensemble suivant est un compact mais n'est pas une intersection fini d'intervalles fermés.
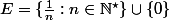
Dans la topologie usuelle, tous les fermés bornés. Ainsi l'ensemble suivant est un compact mais n'est pas une intersection fini d'intervalles fermés.
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: compacts de IR
Soit u une suite de {1/n ; n dans IN*}U{0}.
Auriez-vous un exemple de suite extraite de u qui converge dans {1/n ; n dans IN*}U{0} ?
Auriez-vous un exemple de suite extraite de u qui converge dans {1/n ; n dans IN*}U{0} ?
Re: compacts de IR
De toute suite on peut extraire une suite monotone.
D'où :
Soit la suite extraite est nulle et c'est gagné.
Soit la suite extraite est croissante non nulle, comme elle prend ses valeurs dans un ensemble discret, elle est constante à partir d'un certain rang.
Soit la suite extraite est décroissante, et alors soit elle minorée par un réel strictement positif et par conséquent elle est constante à partir d'un certain rang, dans le cas contraire elle converge vers zéro.
On peut le voir sans le théorème de la suite extrait monotone : si la suite est minorée à partir d'un certain rang par un réel strictement positif, elle prend ses valeurs dans un ensemble fini on peut donc aisément lui extraire une suite convergente. Sinon on peut extraire une suite convergent vers zéro.
D'où :
Soit la suite extraite est nulle et c'est gagné.
Soit la suite extraite est croissante non nulle, comme elle prend ses valeurs dans un ensemble discret, elle est constante à partir d'un certain rang.
Soit la suite extraite est décroissante, et alors soit elle minorée par un réel strictement positif et par conséquent elle est constante à partir d'un certain rang, dans le cas contraire elle converge vers zéro.
On peut le voir sans le théorème de la suite extrait monotone : si la suite est minorée à partir d'un certain rang par un réel strictement positif, elle prend ses valeurs dans un ensemble fini on peut donc aisément lui extraire une suite convergente. Sinon on peut extraire une suite convergent vers zéro.
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 61 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
